Calculate Standard Deviation For Probability Distributions: A Step-By-Step Guide
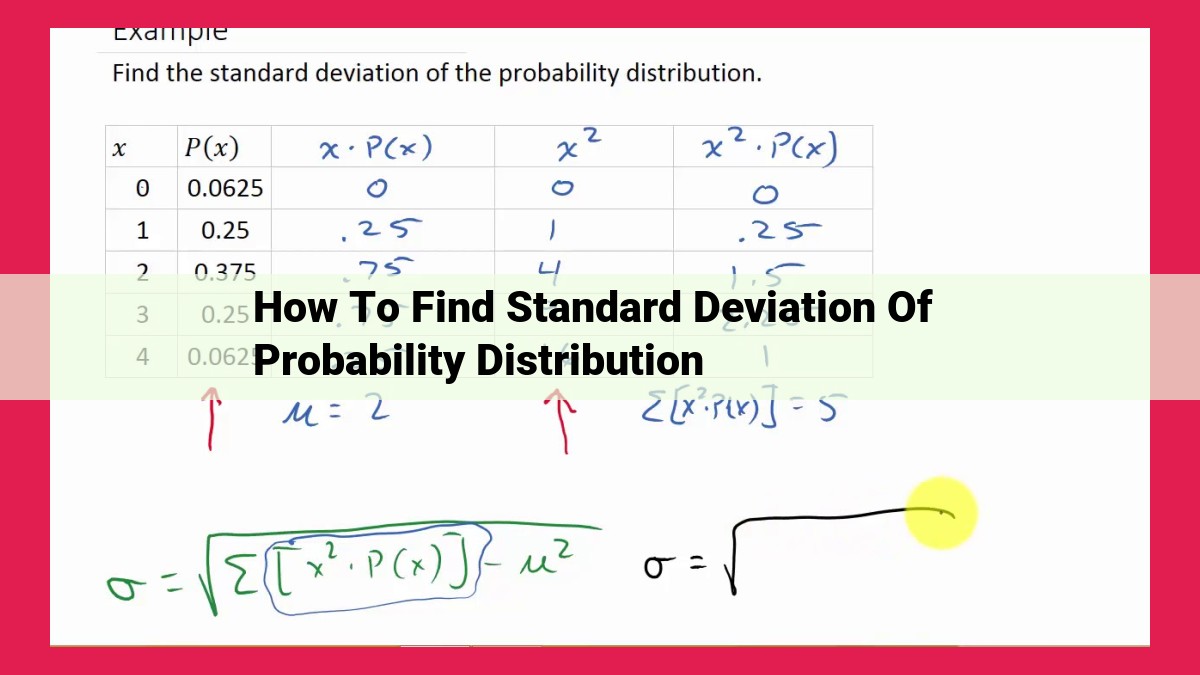
To find the standard deviation of a probability distribution, first determine the mean (average) of the distribution. Then, calculate the variance by summing the squared differences between each data point and the mean, then dividing by the number of data points. Finally, take the square root of the variance to obtain the standard deviation. This measure quantifies the dispersion of data points around the mean, indicating variability and the reliability of predictions based on the distribution.
Understanding Standard Deviation in Probability
In the realm of probability, standard deviation emerges as a crucial tool for quantifying the variability or dispersion of data. It provides insights into how spread out a set of data is and helps us understand how much individual values deviate from the central tendency (mean).
Importance of Standard Deviation
Standard deviation serves as a cornerstone in statistics, enabling researchers to:
- Determine the consistency and reliability of datasets
- Compare different distributions
- Make informed decisions based on data analysis
- Predict future outcomes and understand the likelihood of events occurring
Types of Standard Deviation
Standard deviation can be classified into two main types:
- Sample Standard Deviation: Calculated for a subset of a population, it estimates the standard deviation of the entire population.
- Population Standard Deviation: Calculated for an entire population, providing the exact value of the data’s variability.
Understanding the Difference
The sample standard deviation, typically denoted by s, is used when only a portion of a population is available. It is calculated using the formula:
s = √[(1 / (n-1)) * ∑(x - μ)^2]
Where:
- n is the sample size
- x is each data point
- μ is the sample mean
The population standard deviation, denoted by σ, is calculated when the entire population is known. It uses the same formula as the sample standard deviation, but the divisor is n instead of (n-1).
Standard deviation is a fundamental statistical measure that provides valuable information about data variability. Understanding its importance and the different types of standard deviation is essential for anyone involved in data analysis, research, and decision-making.
Types of Standard Deviation
Understanding the two primary types of standard deviation is crucial: sample standard deviation and population standard deviation.
Sample Standard Deviation
When dealing with a sample, which is a subset of a larger population, we rely on the sample standard deviation, symbolized as ‘s’. Its formula involves calculating the differences between each data point and the sample mean, then squaring and averaging these differences. Finally, the square root of this average is the sample standard deviation.
The calculation of the sample standard deviation is vital as it provides a measure of how much the data in a sample varies from the sample mean. A higher sample standard deviation indicates greater variability within the sample, while a lower standard deviation indicates less variability.
Population Standard Deviation
In contrast, the population standard deviation, represented by the Greek letter ‘sigma’ (σ), applies to the entire population of data, not just a sample. It uses a similar formula, but instead of the sample mean, it uses the true population mean. However, since it’s often challenging to obtain data on an entire population, the population standard deviation is rarely calculated directly.
Instead, we often estimate it using the sample standard deviation. If we have a large enough sample, the sample standard deviation will provide a good approximation of the population standard deviation.
Variance: A Deeper Dive into Data Variability
In the realm of probability, understanding variance is crucial for deciphering the nuances of data variability. Variance is a statistical measure that quantifies the spread or dispersion of data points around the mean or average.
The Relationship with Standard Deviation
Variance and standard deviation are intimately related. In fact, standard deviation is simply the square root of variance. This means that a higher variance corresponds to a larger standard deviation, indicating greater data dispersion. Conversely, a smaller variance translates to a smaller standard deviation and less data variability.
Variance and Data Understanding
Variance plays a pivotal role in comprehending the distribution of data. It provides insights into how data points are distributed across a range of values. A higher variance implies that the data points are spread out over a wider range, while a lower variance indicates that the data points are clustered more closely around the mean.
By analyzing variance, researchers can gain valuable information about the underlying patterns and variability within a dataset. This knowledge can be used to make informed decisions, identify trends, and predict future outcomes.
Mean’s Role in Unraveling Standard Deviation
When embarking on the journey of data analysis, one crucial concept that arises is standard deviation. This enigmatic measure quantifies the dispersion of data points, providing invaluable insights into the variability of your dataset. At the heart of standard deviation calculation lies the concept of mean, an equally indispensable statistical tool.
The mean, also known as the average, is a central measure that represents the typical value of a dataset. It’s calculated by summing up all the values and dividing the result by the number of data points. The mean acts as a reference point against which we gauge the spread of the data.
Standard deviation measures how far data points deviate from the mean. High standard deviation indicates significant data spread, while a low standard deviation suggests data points clustering closer to the mean. The mean provides the baseline for this measurement.
Consider this analogy: Imagine a group of archery targets with varying distances from the bullseye. The mean distance represents the average distance of all the targets. Standard deviation, in this scenario, would be the measure of how much each target’s distance deviates from the mean.
In the world of probability distributions, the mean plays an even more crucial role. The normal distribution, a bell-shaped curve that underpins many statistical models, relies heavily on the mean and standard deviation to define its shape and spread.
Understanding the interplay between mean and standard deviation enables us to make informed decisions about data analysis and interpretation. It empowers us to draw meaningful inferences, make predictions, and ultimately harness the power of statistics to unravel the secrets hidden within our data.
Types of Frequency Distributions: Unveiling the Patterns within Your Data
In the realm of statistics, frequency distributions play a pivotal role in visualizing and understanding the distribution of data. These distributions are graphical representations that depict the number of times each unique value appears within a dataset. By examining frequency distributions, we can uncover patterns and gain insights into the behavior of our data.
Discrete Frequency Distributions
Discrete frequency distributions are employed when the data takes on distinct, whole number values. In these distributions, each value represents a specific category or event. For example, the number of heads obtained when flipping a coin can be represented using a discrete frequency distribution, where each category represents the number of heads obtained (0, 1, or 2).
Continuous Frequency Distributions
Unlike discrete distributions, continuous frequency distributions are used to represent data that can take on any value within a range. The data values in such distributions are typically measurements, such as height, weight, or temperature. Continuous frequency distributions use histograms to visualize the distribution of data, with each bar representing a specific interval of values.
Shapes of Frequency Distributions
Frequency distributions can exhibit various shapes, which provide important information about the underlying data. Some common shapes include:
- Normal Distribution: A bell-shaped distribution that represents data that is symmetric and centered around the mean.
- Uniform Distribution: A flat distribution where all values occur with equal frequency.
- Skewed Distribution: A distribution that is not symmetric, with either a positive or negative skew.
- Bimodal Distribution: A distribution that has two distinct peaks, indicating the presence of two different groups or populations within the data.
Benefits of Frequency Distributions
Frequency distributions offer numerous benefits:
- Data Visualization: They provide a visual representation of the distribution of data, making it easier to identify patterns and outliers.
- Data Summary: They condense large datasets into a manageable format, providing a snapshot of the overall distribution.
- Hypothesis Testing: Different shapes of frequency distributions can provide clues about the underlying population and support or refute statistical hypotheses.
Understanding the Power of Frequency Distributions
By analyzing frequency distributions, we can gain valuable insights into our data and make informed decisions. They help us understand the variability, central tendency, and shape of our data, enabling us to draw meaningful conclusions and make predictions about future outcomes.
Probability Distributions: Unveiling the Patterns in Data
Probability distributions play a crucial role in predicting outcomes and unlocking insights into the behavior of data. They are mathematical functions that describe the likelihood of different values occurring in a random variable. These distributions provide a framework for understanding the shape, spread, and central tendency of data.
Types of Probability Distributions
There are various types of probability distributions, each with unique characteristics:
- Normal Distribution: The ubiquitous bell-shaped curve that represents many natural phenomena, from heights to test scores.
- Uniform Distribution: A distribution where all values within a specific range are equally likely.
- Exponential Distribution: Describes the time between random events, such as the time between customer arrivals at a store.
- Binomial Distribution: Used to model the number of successes in a fixed number of independent trials, like coin flips or dice rolls.
Significance of Probability Distributions
Probability distributions offer invaluable insights for:
- Predicting Outcomes: They enable researchers and analysts to forecast the likelihood of future events, such as the success of a new product or the occurrence of a rare disease.
- Estimating Risks: Probability distributions help assess the risk associated with decisions, enabling businesses and individuals to make informed choices.
- Modeling Data: They provide a framework for fitting data to a known distribution, allowing for accurate predictions and comparisons.
- Statistical Inferences: Probability distributions form the basis for statistical hypothesis testing and confidence intervals, which help researchers draw conclusions about populations based on sample data.
Properties of Normal Distribution
- Characteristics and properties of the normal distribution
- Role of the normal distribution in finding standard deviation
Properties of the Normal Distribution: The Bell Curve’s Central Role
In the realm of probability and statistics, the normal distribution, also known as the bell curve, occupies a central position. Its well-defined characteristics and properties make it a valuable tool for understanding and analyzing data.
Characteristics of the Normal Distribution
The normal distribution is characterized by its symmetrical bell-shaped curve. This means that data tends to cluster around the mean (average) value, with a gradual decrease in frequency as you move away from the mean in either direction. The curve is also continuous, meaning that it does not have any jumps or gaps.
Role in Finding Standard Deviation
The normal distribution plays a vital role in determining the standard deviation, a measure of how spread out the data is. The standard deviation is calculated using a formula that takes into account the differences between each data point and the mean. In a normal distribution, approximately two-thirds of the data falls within one standard deviation of the mean, while the remaining two-thirds falls within two standard deviations.
Key Properties
Some key properties of the normal distribution include:
- Symmetry: The distribution is symmetrical around the mean, meaning that the curve is mirrored on both sides of the mean.
- Modality: The distribution has a single peak (mode) at the mean.
- Area Under the Curve: The total area under the normal curve is always equal to 1, representing the probability of an event occurring.
- Empirical Rule (68-95-99.7 Rule): In a normal distribution, about 68% of data falls within one standard deviation of the mean, 95% within two standard deviations, and 99.7% within three standard deviations.
The normal distribution is a fundamental concept in probability and statistics. Its characteristics and properties, including its bell-shaped curve and its role in finding the standard deviation, make it a powerful tool for analyzing and understanding data. By understanding the nature of the normal distribution, researchers and analysts can gain valuable insights into the patterns and trends within their data.
Central Limit Theorem and Its Implications
Imagine you have a coin and you flip it multiple times. Would you expect the outcomes to be perfectly balanced, with an equal number of heads and tails? Not necessarily. In fact, even if the coin is fair, it is unlikely to land with perfect symmetry. The Central Limit Theorem helps us understand why.
Statement of the Central Limit Theorem:
The Central Limit Theorem states that as the sample size of a population increases, the distribution of sample means approaches a normal distribution, regardless of the original population distribution. In other words, even if the underlying data is skewed or highly variable, the average of a large enough sample will tend to follow a bell-shaped curve.
Implications for Finding Standard Deviation:
The Central Limit Theorem has important implications for finding standard deviation. Since the sample means are normally distributed, we can use the properties of the normal distribution to determine the standard deviation of the sample means. The standard deviation of sample means (also known as the standard error of the mean) is given by:
Standard Error of the Mean = Standard Deviation of Population / Square Root of Sample Size
This formula allows us to estimate the standard deviation of the population even when we do not have access to the entire population. It is a valuable tool for making inferences about a population based on sample data.