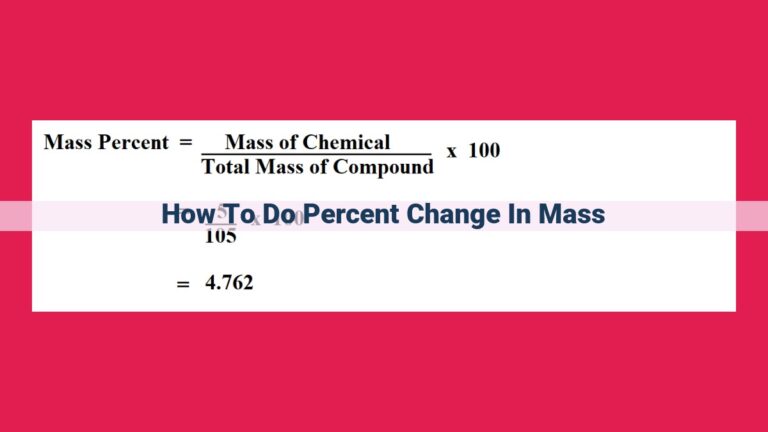Calculate Relative Density Percentage: Compare Substance Mass To Water Density

Relative density percentage compares the density of a substance to the density of water, offering a measure of its relative weight. To calculate it, divide the substance’s mass by its volume, then divide this value by the density of water (1 g/mL). Multiply the result by 100 to express it as a percentage. This percentage indicates how much denser or lighter the substance is than water, with values above 100 indicating greater density and values below 100 indicating lesser density.
Understanding Relative Density Percentage
In the realm of science and engineering, the concept of relative density percentage plays a crucial role in characterizing and comparing substances. It delves into the intricate relationship between density, mass, volume, and buoyancy, providing valuable insights into the properties of materials.
Density, a fundamental property of matter, measures the compactness of a substance. It is defined as the ratio of its mass to its volume. The mass of an object represents the amount of matter it contains, while its volume quantifies the space it occupies. The buoyancy of a substance refers to its tendency to float or sink in a fluid due to the opposing forces of gravity and upward pressure exerted by the fluid.
By considering the density of a substance relative to a reference substance, typically water, we arrive at the concept of relative density. This dimensionless quantity is often expressed as specific gravity, a term used interchangeably with relative density. A relative density greater than 1 indicates that the substance is denser than water and will sink in it. Conversely, a relative density less than 1 indicates that the substance is less dense than water and will float on its surface.
To calculate the relative density percentage of a substance, we use the formula:
Relative Density Percentage = (Density of Substance / Density of Reference Substance) x 100%
This formula expresses the relative density as a percentage, providing a convenient way to compare the density of different substances. It is important to note that the reference substance is typically water, which has a density of 1 gram per cubic centimeter (g/cm³).
Understanding relative density percentage is crucial in various fields, including chemistry, engineering, and geology. It helps in identifying and characterizing minerals, predicting the behavior of fluids in different environments, and designing buoyancy-based devices such as submarines and hot air balloons.
Density: Unraveling the Relationship Between Mass, Volume, and Buoyancy
In the realm of physics, understanding the properties of matter is crucial. Among these properties, density plays a pivotal role in characterizing various materials. It’s a measure of how compactly matter is packed together, intricately related to an object’s mass and volume.
Mass, Volume, and the Essence of Density
Mass, measured in grams, kilograms, or pounds, represents the quantity of matter in an object. Volume, expressed in cubic centimeters, cubic meters, or gallons, indicates the amount of space occupied by that matter. Density then emerges as the ratio between an object’s mass and its volume.
D = m/V
Where:
- D represents density
- m represents mass
- V represents volume
This equation reveals that density is directly proportional to mass and inversely proportional to volume. Therefore, a denser object has more mass packed into a smaller volume, while a less dense object has less mass distributed over a larger volume.
Buoyancy and the Dance of Density
The concept of buoyancy further illuminates the interplay between mass, volume, and density. Buoyancy refers to the upward force exerted by a fluid that opposes the weight of an immersed object. This force is directly proportional to the density of the fluid and the volume of the object displaced.
When an object is submerged in a fluid, it experiences an upward buoyant force that counteracts its downward gravitational force. If the density of the object is greater than the density of the fluid, the object will sink. Conversely, if the density of the object is less than the density of the fluid, the object will float.
This phenomenon allows us to determine the density of an object by measuring the force required to keep it suspended in a fluid of known density. For instance, a hydrometer is a device used to measure the density of liquids by exploiting the principles of buoyancy.
Example:
An object with a mass of 10 grams and a volume of 2 cubic centimeters is submerged in water. The density of water is 1 gram per cubic centimeter.
- Density of the object = 10 grams / 2 cubic centimeters = 5 grams per cubic centimeter
Since the density of the object is greater than the density of water, the object will sink.
Relative Density: Understanding Density and Specific Gravity
Understanding density is crucial when comparing the physical properties of different substances. Relative density measures how an object’s density compares to that of water, making it a valuable tool in various scientific fields.
Specific gravity is an alternative term for relative density. It expresses the density of a substance relative to the density of water at 4°C, which is 1 g/cm³. Hence, if a substance has a specific gravity of 0.5, its density is half that of water.
Calculating Relative Density
The formula for calculating relative density is:
Relative density = Density of substance / Density of reference substance
For liquids and solids, the reference substance is typically water, with a density of 1 g/cm³.
Example Calculation
Let’s say we want to find the relative density of a liquid with a density of 0.85 g/cm³. Using the formula:
Relative density = 0.85 g/cm³ / 1 g/cm³ = 0.85
Therefore, the relative density of the liquid is 0.85, indicating that it is less dense than water.
Understanding Percentage: A Step towards Accurate Relative Density Calculations
When dealing with the concept of relative density percentage, it’s essential to have a firm grasp on the concept of percentage. Percentage, a term often encountered in everyday life, allows us to express a value as a proportion of another. It’s a powerful tool that simplifies calculations and helps us understand the relative magnitude of values.
In its essence, percentage is a fraction represented as a hundredth part of a whole. It’s written as “x%”, where “x” represents the number of parts per hundred. To calculate percentage, we use the formula:
Percentage = (Part / Whole) x 100
For example, if we have 20 out of 100 parts, the percentage can be calculated as:
Percentage = (20 / 100) x 100 = 20%
This means that 20 represents 20 parts out of 100, or one-fifth of the whole.
Percentage plays a crucial role in calculating relative density percentage, a concept we’ll explore in the next section. By understanding percentage, we can accurately determine the density of an object relative to a reference substance, typically water. This knowledge is invaluable in various fields, from chemistry to engineering.
Understanding Relative Density Percentage: The Formula and Its Significance
When it comes to characterizing materials, their density plays a pivotal role. Density measures the compactness of matter within a given volume, indicating how much mass is packed into its space.
Relative density takes this concept a step further. It compares the density of a substance with the density of a reference substance, usually water. This comparison provides a convenient way to quantify the heaviness or lightness of different materials.
To calculate relative density percentage, we use the following formula:
Relative Density Percentage = (Density of Substance / Density of Reference Substance) x 100%
The density of the reference substance is typically water and is considered to be 1 g/mL.
For instance, if a substance has a density of 0.8 g/mL, its relative density percentage would be:
Relative Density Percentage = (0.8 g/mL / 1 g/mL) x 100% = 80%
This calculation shows that the substance is 80% as dense as water.
Understanding relative density percentage is essential for various scientific, engineering, and industrial applications. It helps us determine the buoyancy of objects, predict the behavior of fluids, and design materials with specific density requirements.
Understanding Relative Density Percentage: A Comprehensive Guide
Relative density percentage, also known as specific gravity, is a crucial concept in understanding the density of substances. It measures the density of a substance relative to water, which is assigned a density of 1. This value helps us compare the mass of a substance to an equal volume of water, providing valuable insights into the substance’s physical properties.
Density: Mass, Volume, and Buoyancy
Density refers to the mass of a substance per unit volume. It is affected by the physical structure and composition of the substance. Buoyancy, on the other hand, is the upward force exerted on an object immersed in a fluid that counteracts the weight of the object. This force plays a significant role in determining the density of an object.
Relative Density: Specific Gravity and Buoyancy
Relative density, also referred to as specific gravity, is a dimensionless quantity that compares the density of a substance to the density of water. A substance with a relative density greater than 1 is denser than water and will sink, while a substance with a relative density less than 1 is less dense than water and will float.
Percentage: Understanding Fractions, Ratios, and Proportions
Percentage is a way of expressing a value as a portion of 100. It represents a fraction or a ratio of a numerator to a denominator, multiplied by 100. This concept is essential for calculating relative density percentage.
Formula for Calculating Relative Density Percentage
The formula for calculating relative density percentage is:
Relative Density Percentage = (Density of Substance / Density of Reference (usually Water)) x 100
Where:
- Density of Substance is the measured density of the substance in grams per milliliter (g/mL) or kilograms per liter (kg/L).
- Density of Reference is the density of the reference substance, typically water, which is 1 g/mL.
Example Calculation
To illustrate the calculation, let’s consider an object with a density of 2.5 g/mL.
Relative Density Percentage = (2.5 g/mL / 1 g/mL) x 100
= 2.5 x 100
= **250%**
This result indicates that the object has a relative density percentage of 250%. It is 2.5 times denser than water and will sink when submerged.
Comprehending the concept of relative density percentage is crucial for accurate calculations and understanding the physical properties of substances. This guide provides a comprehensive overview of the underlying principles, empowering readers to apply these concepts in various applications across scientific and industrial fields.