Focal Length Calculation: Essential Equations for Lens Focusing

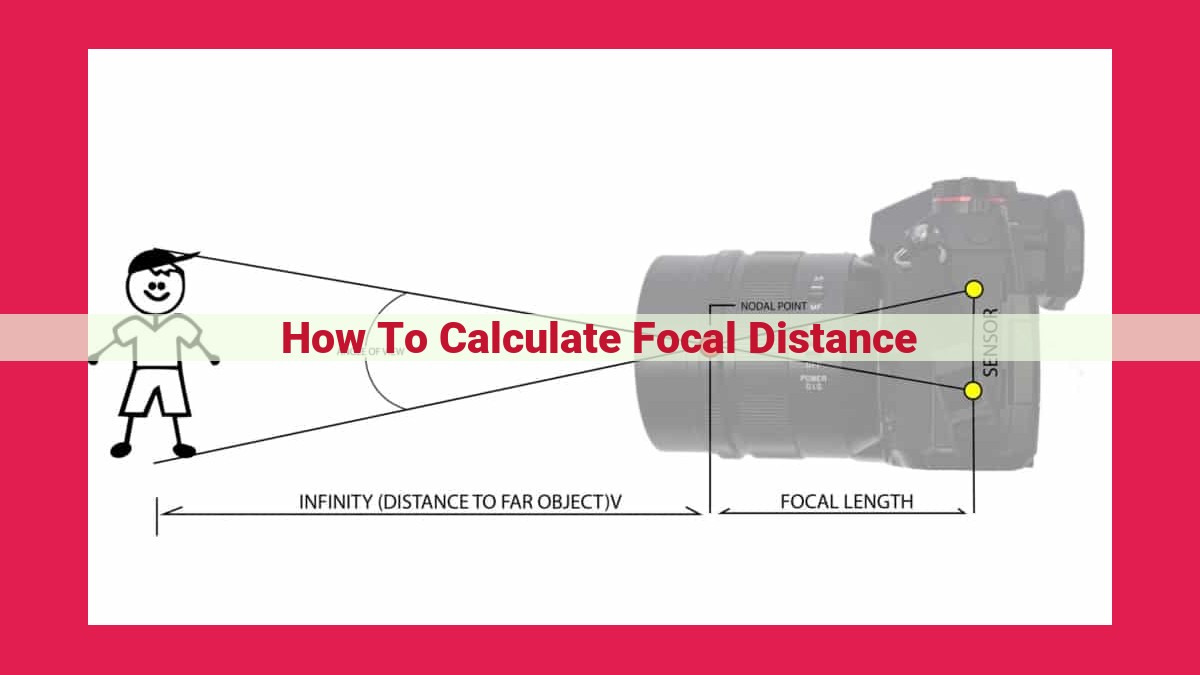
To calculate focal distance, you can use the Thin Lens Equation (1/do + 1/di = 1/f) which relates object distance (do), image distance (di), and focal length (f). Alternatively, the Lensmaker’s Equation (1/f = (n-1) * [(1/R1) + (1/R2)]) calculates focal length based on refractive index (n) and radii of curvature (R1, R2). Focal length determines lens focusing.

Contents

Lenses: Unraveling the Secrets of Light Bending

In the realm of optics, lenses hold a central place, bending and focusing light to create images that shape our perception of the world. To master the art of lens design and manipulation, understanding the fundamental principles that govern their behavior is paramount. Let’s embark on a journey to unveil the secrets of lenses, starting with the cornerstone of lens optics – the thin lens equation.

The Thin Lens Equation: Connecting Object, Image, and Focal Length

At the heart of thin lens optics lies a simple yet profound equation:

**1/do + 1/di = 1/f**

This equation is a testament to the lensmaker’s craft, linking three crucial parameters:

Object distance (do): The distance between the object and the lens.
Image distance (di): The distance between the image and the lens.
Focal length (f): A fundamental property of the lens that determines its focusing power.

The Lensmaker’s Equation: Shaping Focal Length

Another pivotal equation in the lensmaker’s toolkit is the lensmaker’s equation:

**1/f = (n-1) * [(1/R1) + (1/R2)]**

This equation reveals the intricate relationship between the lens’s focal length (f) and its physical characteristics:

Refractive index (n): A measure of how much light bends when passing through the lens material.
Radii of curvature (R1 and R2): The radii of the two curved surfaces of the lens.

A Deeper Dive into Lens Parameters

To delve deeper into the workings of lenses, let’s dissect each parameter in the thin lens equation:

Object distance (do) determines whether the object is in front of or behind the lens and whether the image is virtual or real.
Image distance (di) indicates where the image is formed and its size relative to the object.
Focal length (f) is a measure of the lens’s focusing power: a shorter focal length means stronger focusing, while a longer focal length results in weaker focusing.

The thin lens equation and lensmaker’s equation provide a powerful framework for understanding and manipulating lenses. By mastering these concepts, we can harness the transformative power of lenses to capture images, correct vision, and explore the wonders of the optical world.

Understanding the Lens Equation: A Journey into Light Manipulation

The Thin Lens Equation: Connecting Distance and Focal Length

Embark on an optical adventure with the Thin Lens Equation, a fundamental formula that governs the behavior of light as it interacts with lenses. This equation, 1/do + 1/di = 1/f, reveals the intricate relationship between the object distance (do), where the object is placed, the image distance (di), where the image forms, and the focal length (f), a characteristic of the lens.

Imagine a lens as a portal through which light travels. The object distance is the distance between the object and the lens, determining the size and location of the virtual image formed by the lens. On the other hand, the image distance is the distance between the image and the lens, defining where the light rays converge after passing through the lens.

The focal length, a crucial property of the lens, is what connects these distances. It represents the distance between the lens and the principal point where parallel rays of light converge after passing through the lens. This inherent characteristic determines the lens’s ability to focus light and create images.

By understanding the Thin Lens Equation, we can unravel the mysteries of image formation, predicting how lenses manipulate light to create different image sizes and orientations. It empowers us to design optical systems, from spectacles to telescopes, that harness the power of lenses to enhance our vision and explore the wonders of light.

Understanding the Lensmaker’s Equation: The Key to Focal Length

In the realm of optics, lenses hold a pivotal role in shaping light and forming images. One fundamental aspect of lens behavior is determined by its focal length, a crucial parameter that governs the lens’s focusing capabilities. The Lensmaker’s Equation provides a powerful tool for understanding how various factors, such as the lens’s refractive index and radii of curvature, come together to determine its focal length.

The Lensmaker’s Equation is a mathematical formula that expresses the relationship between the focal length (f), the refractive index (n) of the lens material, and the radii of curvature (R1 and R2) of the lens’s surfaces:

1/f = (n-1) * [(1/R1) + (1/R2)]

This equation reveals that the focal length of a lens is not a fixed property but is instead influenced by three key factors:

Refractive Index (n): The refractive index is a dimensionless quantity that describes how much light bends when passing through a material. The higher the refractive index, the more light is bent.
Radii of Curvature (R1 and R2): The radii of curvature are the distances from the centers of curvature of the lens surfaces to the lens itself. Lenses can have positive or negative radii; a positive radius indicates a convex surface, while a negative radius indicates a concave surface.

By understanding the interplay between refractive index, radii of curvature, and focal length, we can gain valuable insights into the behavior of lenses. For example, a lens with a high refractive index will bend light more sharply, leading to a shorter focal length. Similarly, a lens with steeper radii of curvature will also have a shorter focal length.

Harnessing the power of the Lensmaker’s Equation empowers us to design and optimize lenses for various applications, from eyeglasses and camera lenses to optical instruments used in telescopes and microscopes. By carefully choosing the refractive index and radii of curvature, we can create lenses with specific focal lengths to meet the unique demands of different optical systems.

Understanding Geometric Optics: A Deep Dive into Lenses

In the realm of optics, lenses play a pivotal role in capturing, focusing, and shaping light. To fully grasp the intricacies of lenses, it’s essential to delve into the fundamental equations and concepts governing their behavior.

The Lensmaker’s Equation: Unveiling the Focal Length

The lensmaker’s equation is a cornerstone in the study of lenses. This equation provides a direct link between the focal length of a lens and its physical properties.

This equation, given as:

1/f = (n - 1) * [(1/R1) + (1/R2)]

where:

f is the focal length
n is the refractive index of the lens material
R1 and R2 are the radii of curvature of the lens surfaces

Refractive Index: A Measure of Light’s Journey

The refractive index of a material is a measure of how it bends light. When light passes from one medium to another, its speed changes, causing it to refract or bend at the interface. The refractive index is calculated as the ratio of the speed of light in a vacuum to its speed in the material.

Radii of Curvature: The Geometry of Lenses

The radii of curvature, denoted as R1 and R2, refer to the radii of the spherical surfaces that make up the lens. These radii determine the shape and convergence of light rays passing through the lens.

Positive radii indicate that the lens surface is convex, while negative radii signify a concave surface. Lenses can have either symmetric (both surfaces having the same curvature) or asymmetric (surfaces with different curvatures) configurations.

The Lensmaker’s Equation in Action

The lensmaker’s equation reveals a profound relationship between the focal length, refractive index, and radii of curvature of a lens. By manipulating these variables, lens makers can create lenses with specific focusing capabilities for various applications.

For example, a lens with a positive focal length is a converging lens that brings parallel light rays to a single point, while a lens with a negative focal length is a diverging lens that causes parallel light rays to appear to originate from a single point.

The lensmaker’s equation is a powerful tool that empowers us to understand the behavior of lenses. By grasping the intricate relationships between its parameters, we can optimize lens design for a wide range of optical applications. From eyeglasses to camera lenses, this equation underpins the advancement of optical technology and our ability to capture and manipulate light.

Understanding the Fundamentals of Optics: A Beginner’s Guide to Lenses

The Thin Lens Equation: Unraveling the Relationship between Object, Image, and Focal Length

The thin lens equation, expressed as 1/do + 1/di = 1/f, where do is the object distance, di is the image distance, and f is the focal length, is a cornerstone of optics. This equation highlights the inverse relationship between object and image distances and the constant focal length of the lens.

Object Distance (do): The Starting Point of Optical Imagery

Object distance (do) refers to the distance between the lens and the object being projected. It is a crucial parameter that determines the image formed by the lens. By understanding the relationship between object distance, image distance, and focal length, optical engineers can manipulate these variables to achieve desired image characteristics.

Image Distance (di): Unveiling the Hidden Image

Image distance (di) represents the distance between the lens and the image formed. Similar to object distance, image distance plays a key role in determining the image’s size, orientation, and clarity. Understanding image distance is essential for optimizing lens positioning and achieving desired optical outcomes.

Focal Length (f): The Magnifying Force behind Lenses

Focal length (f) is an inherent property of a lens that determines magnification. It represents the distance between the lens and the point where parallel rays of light converge after passing through the lens. Understanding focal length is critical for selecting lenses with the appropriate magnifying power for specific applications.

Explain its role in the thin lens equation.

Understanding Lens Equations for Enhanced Photography

In the realm of photography, lenses play a pivotal role in capturing stunning images. Understanding the underlying equations that govern lens behavior is essential for photographers to master the art of image creation. Let’s delve into three crucial lens equations: the Thin Lens Equation, the Lensmaker’s Equation, and their key components.

1. The Thin Lens Equation

The Thin Lens Equation is a fundamental equation that describes the relationship between the object distance, image distance, and focal length of a lens. It’s expressed as:

1/do + 1/di = 1/f

Where:

do is the distance between the lens and the object (measured in meters)
di is the distance between the lens and the image (measured in meters)
f is the focal length of the lens (measured in meters)

The equation reveals that as the object distance increases, the image distance decreases, and vice versa. This property is crucial in controlling the size and location of the image formed by the lens.

2. The Lensmaker’s Equation

The Lensmaker’s Equation calculates the focal length of a lens based on its refractive index and radii of curvature. It’s given by:

1/f = (n-1) * [(1/R1) + (1/R2)]

Where:

f is the focal length of the lens (measured in meters)
n is the refractive index of the lens material
R1 and R2 are the radii of curvature of the lens surfaces (measured in meters)

This equation demonstrates that the focal length of a lens depends on its refractive index and the shape of its surfaces. By manipulating these factors, lens designers can create lenses with specific focal lengths for various applications.

3. Object Distance and Image Distance

In both the Thin Lens Equation and the Lensmaker’s Equation, the object distance and image distance play critical roles. The object distance, do, represents the distance between the object and the lens. The image distance, di, represents the distance between the lens and the image. These distances determine the magnification and sharpness of the image formed by the lens.

Delving into the World of Lenses: Unraveling the Secrets of Image Distance

In the realm of optics, understanding image distance (di) is crucial for comprehending how lenses shape light to produce clear images. It is one of the fundamental parameters that define the characteristics of a lens system.

What is Image Distance?

Image distance is the distance between the lens and the point where the image is formed. It is measured from the optical center of the lens to the image plane. When an object is placed at a certain distance from the lens, the object distance (do), the light rays emerging from the object converge at a point on the opposite side of the lens. This point of convergence is known as the image, and its distance from the lens is di.

The Thin Lens Equation and Image Distance

The relationship between image distance, object distance, and focal length (f) is governed by the thin lens equation:

1/do + 1/di = 1/f

This equation tells us that the reciprocals of object distance and image distance add up to the reciprocal of the focal length. Manipulating this equation, we can solve for image distance:

di = (f * do) / (do - f)

Importance of Image Distance

Image distance plays a vital role in determining the magnification and size of the image formed by a lens. A smaller image distance indicates a larger magnification, meaning the image will be larger than the object. Conversely, a larger image distance results in a smaller magnification, producing an image that is smaller than the object.

By adjusting the object distance or the focal length of the lens, we can control the image distance and hence, the magnification. This principle is used in various optical instruments, such as microscopes, telescopes, and cameras, to achieve the desired image size and detail.

Exploring the Intriguing World of Lenses: A Simple Guide to Lens Equations

Imagine you’re on an exciting adventure, venturing into the fascinating world of optics. Your trusty guide, a knowledgeable lens, will accompany you on this journey to unravel the mysteries of lens equations.

The Thin Lens Equation: A Tale of Distances

Our first stop in this optical saga is the thin lens equation. It’s like a magical formula that connects three crucial characters: object distance (do), image distance (di), and focal length (f).

The equation reads like a riddle:

1/do + 1/di = 1/f

It tells us that the inverse of the object distance plus the inverse of the image distance equals the inverse of the focal length.

Object Distance: The Lens’s Starting Point

The object distance is like the starting line for our lens’s adventure. It measures how far away the object is located from the lens. Whether it’s the page of a book or the bird flying outside, the object’s distance to the lens determines where the image will form.

Image Distance: The Lens’s Goal

The image distance is our lens’s goal. It tells us how far away the image is formed from the lens. This distance depends on the object’s distance and the focal length of the lens.

Together, the object distance and the image distance govern the lens’s ability to focus an image. By adjusting either of these distances, we can control where the image appears.

Understanding the World of Lenses: A Guide to Lens Equations

Embark on a journey into the captivating realm of optics, where lenses play a pivotal role in manipulating light and shaping our perception of the world. Join us as we delve into the fundamental lens equations that govern the intricate dance of light rays, exploring their intriguing relationships and illuminating the principles that underpin lens behavior.

The Thin Lens Equation: A Keystone of Lens Understanding

At the heart of lens theory lies the thin lens equation, a mathematical formula that serves as a cornerstone in understanding the behavior of light as it passes through a lens. This equation, expressed as 1/do + 1/di = 1/f, elegantly relates the object distance (do), image distance (di), and focal length (f). By grasping this equation, we gain insight into how lenses transform the path of light, creating images and shaping our vision.

Object Distance: Defining the Lens’s Starting Point

The object distance, denoted by do, represents the distance between the object and the center of the lens. It is the initial position of the object before the light rays enter the lens and embark on their optical adventure. This distance plays a crucial role in determining the image’s location and characteristics.

Image Distance: Unveiling the Image’s Destination

The image distance, symbolized by di, marks the location of the image formed by the lens. It measures the distance between the image and the center of the lens, revealing where the light rays converge after passing through the lens. Understanding the image distance is essential for predicting the size and orientation of the image.

Focal Length: The Lens’s Inherent Characteristic

The focal length, represented by f, is an intrinsic property of the lens that governs its focusing ability. It determines the ability of the lens to bend light rays and create images. Shorter focal lengths result in stronger bending of light, leading to images that are larger and closer to the lens, while longer focal lengths produce smaller, more distant images.

The Lensmaker’s Equation: Unraveling the Secrets of Lens Design

The lensmaker’s equation, expressed as 1/f = (n-1) * [(1/R1) + (1/R2)], offers a deeper understanding of how the lens’s design influences its focal length. Here, n denotes the refractive index of the lens material, which describes its ability to bend light, while R1 and R2 represent the radii of curvature of the lens’s two surfaces. Exploring this equation unveils the intricate interplay between lens design and its optical properties.

The Thin Lens Equation: A Window into Optics

In the realm of optics, understanding the thin lens equation is paramount. This equation, represented as 1/do + 1/di = 1/f, provides a fundamental relationship between object distance (do), image distance (di) and focal length (f). It allows us to predict the behavior of light as it passes through a lens, enabling us to design and use optical instruments effectively.

The Interplay of Distances and Focal Length

Imagine a thin lens separating an object and its image. Object distance refers to the distance between the object and the lens, while image distance indicates the distance between the image and the lens. The focal length of the lens determines its ability to converge or diverge light rays, ultimately affecting the size and position of the image.

Using the thin lens equation, we can calculate the object and image distances for a given focal length. This understanding is crucial in lens focusing, allowing us to adjust the lens to obtain a clear image at a specific distance. For instance, in a camera, changing the focal length of the lens alters the focus, allowing us to capture images of objects at varying distances.

Lensmaker’s Equation: Unveiling the Focal Length

The lensmaker’s equation provides another valuable insight into lens behavior. This equation, expressed as 1/f = (n-1) * [(1/R1) + (1/R2)], relates the focal length (f), refractive index (n) of the lens material, and radii of curvature (R1 and R2) of the lens surfaces.

The refractive index represents the speed of light in the lens material compared to its speed in a vacuum. The radii of curvature describe the curvature of the lens surfaces. By manipulating these factors, lens designers can create lenses with specific focal lengths for various applications, such as eyeglasses, telescopes, and microscopes.

Additional Insights

Object Distance: The closer the object is to the lens, the farther the image will be and vice versa.
Image Distance: A positive image distance indicates a real image that can be projected onto a screen, while a negative image distance represents a virtual image that cannot be physically captured.
Focal Length: A shorter focal length results in a larger image and a wider field of view, while a longer focal length yields a smaller image and a narrower field of view.
Refractive Index: A higher refractive index typically results in a shorter focal length.
Radii of Curvature: The radii of curvature determine the overall shape of the lens and influence its focal length.

Lens Equations and Properties: The Foundations of Optics

In the realm of optics, lenses play a crucial role in manipulating light and forming images. To fully grasp the behavior of lenses, it’s essential to understand the underlying equations and properties that govern their functioning. Here’s a comprehensive guide to these fundamental concepts:

The Thin Lens Equation

At the heart of lens optics is the thin lens equation:

1/do + 1/di = 1/f

Object distance (do) is the distance between the object and the lens.

Image distance (di) is the distance between the lens and the image.

Focal length (f) is a characteristic of the lens that determines its focusing power.

The thin lens equation reveals the inverse relationship between object distance, image distance, and focal length. As one distance increases, the other decreases.

The Lensmaker’s Equation

The lensmaker’s equation provides a means to calculate the focal length of a lens based on its geometric properties:

1/f = (n-1) * [(1/R1) + (1/R2)]

Refractive index (n) is a measure of how much light bends when passing through the lens material.

Radii of curvature (R1 and R2) are the radii of the two curved surfaces of the lens.

The lensmaker’s equation demonstrates that the focal length of a lens depends on the refractive index of the lens material and the curvature of its surfaces. By manipulating these parameters, lens designers can create lenses with specific focal lengths for various applications.

Object Distance

Object distance (do) is the distance from an object to the lens. It plays a key role in determining the image distance and the size of the image formed by the lens.

Image Distance

Image distance (di) is the distance from the lens to the image. Similar to object distance, image distance is instrumental in calculating image size and understanding the image formation process.

Focal Length

focal length (f) is the distance between the lens and the point where parallel rays of light converge after passing through the lens. It’s a crucial lens property that determines the lens’s focusing ability. Lenses with shorter focal lengths focus light more strongly, while those with longer focal lengths focus light less strongly.

Refractive Index

Refractive index (n) is a measure of how much light bends when passing from one material to another. In the context of lens optics, the refractive index plays a critical role in determining the focal length of the lens, as it affects how strongly light is bent within the lens material.

Radii of Curvature

Radii of curvature (R1 and R2) are the radii of the two curved surfaces of the lens. These parameters are crucial in calculating the focal length of the lens, as the curvature of the lens surfaces directly influences how light is refracted within the lens.

Understanding the Lensmaker’s Equation: How Refractive Index Impacts Focal Length

Why the Focus Matters: Eyeglasses and Magnifying Glasses

Imagine struggling to read a book or focus on a distant object. Eyeglasses and magnifying glasses, tools for vision enhancement, employ lenses to manipulate light and provide clear vision. These lenses have a crucial property called focal length, which determines their ability to focus light.

The Lensmaker’s Equation: Unraveling the Magic of Lenses

The lensmaker’s equation, a formula for focal length, relates the focal length (f) of a lens to its refractive index (n) and radii of curvature (R1 and R2). In essence, it unravels the secret behind how lenses focus light.

Formula: 1/f = (n-1) * [(1/R1) + (1/R2)]

Refractive Index (n): This dimensionless quantity represents how much light is bent when passing through a material.
Radii of Curvature (R1 and R2): These are the radii of the curved surfaces of the lens. R1 is the radius of the surface facing the object, while R2 is the radius of the surface facing the image.

Refractive Index: The Invisible Lens Modifier

The refractive index plays a significant role in determining the focal length of a lens. Materials with higher refractive indices bend light more sharply, resulting in a shorter focal length. Conversely, materials with lower refractive indices bend light less, resulting in a longer focal length.

For instance, glass has a higher refractive index than air. Hence, a glass lens can bend light more effectively, leading to a shorter focal length. This effect is important in creating lenses for eyeglasses and magnifying glasses.

Lenses in Action: Bending Light to Perfect Vision

Lenses with shorter focal lengths converge light rays more strongly, allowing them to focus on objects closer to the lens. This property makes them ideal for magnifying glasses, allowing us to see small objects in greater detail.

In contrast, lenses with longer focal lengths converge light rays less strongly, directing them towards a point further away. This makes them suitable for eyeglasses used to correct conditions like nearsightedness and farsightedness.

In summary, the lensmaker’s equation provides a powerful tool to understand how lenses manipulate light and create clear images. By considering the refractive index and radii of curvature, we can tailor lenses to specific applications, enabling us to see the world in sharper focus.

Dive into the Realm of Lenses: A Comprehensive Guide to Lens Equations and Parameters

In the fascinating world of optics, lenses play a pivotal role in shaping light and capturing images. Understanding the principles governing their behavior is crucial for exploring the intricacies of photography, microscopy, and other optical applications. This article will delve into the essential lens equations and parameters, providing a comprehensive guide for both beginners and enthusiasts alike.

The Thin Lens Equation: A Balancing Act of Distance and Focal Length

The thin lens equation establishes a fundamental relationship between the distance between an object and its image, and the focal length of the lens. Represented by the equation 1/do + 1/di = 1/f, it elegantly expresses the interplay between object distance (do), image distance (di), and focal length (f).

The Lensmaker’s Equation: Crafting Lenses with Desired Properties

Moving beyond the thin lens equation, the lensmaker’s equation offers a means to calculate the focal length of a lens based on its refractive index and the radii of curvature of its surfaces. Given as 1/f = (n-1) * [(1/R1) + (1/R2)], it allows lens designers to create lenses with specific properties tailored to various applications.

Object Distance: The Source of Light

The object distance (do) represents the distance between the object and the lens. It plays a critical role in determining the size and position of the image formed by the lens. Understanding the concept of object distance is essential for controlling the magnification and field of view in optical systems.

Image Distance: Capturing the Image

The image distance (di) measures the distance between the lens and the image it produces. Closely linked to the object distance, it is crucial in determining the type of image formed (real or virtual) and its characteristics. Mastering the concept of image distance enables precise image formation and manipulation in optical devices.

Focal Length: The Heart of the Lens

The focal length (f) is an intrinsic property of a lens that determines its ability to focus light. Represented in millimeters, it dictates the magnification and angle of view of the lens. Understanding focal length is fundamental for selecting the appropriate lens for different photographic and optical applications.

Refractive Index: Bending Light to Your Will

The refractive index (n) plays a crucial role in the lensmaker’s equation. It quantifies the ability of a material to bend light. Different materials possess varying refractive indices, which directly affects the focal length of lenses made from those materials.

Radii of Curvature: Shaping the Lens

The radii of curvature (R1 and R2) describe the curvature of the lens surfaces. They influence the focal length of the lens and contribute to the overall image quality. By manipulating the radii of curvature, lens designers can create lenses with specific aberration correction and other desired optical properties.

Lens Equations and the Fundamentals of Optics

Embark on a journey into the world of optics, where lenses hold the power to unravel the mysteries of light and vision. Let’s begin with two fundamental equations that govern the behavior of lenses: the thin lens equation and the lensmaker’s equation.

The Thin Lens Equation: Unraveling Object and Image Distances

The thin lens equation, 1/do + 1/di = 1/f, establishes a crucial relationship between the object distance (do), the image distance (di), and the lens’s focal length (f).

Object distance (do) is the distance between the object and the lens, while image distance (di) represents the distance between the image and the lens. The focal length (f) is a characteristic property of the lens that determines its ability to focus light.

The Lensmaker’s Equation: Crafting the Focal Length

The lensmaker’s equation, 1/f = (n-1) * [(1/R1) + (1/R2)], provides a formula for calculating the focal length of a lens based on its refractive index (n) and radii of curvature (R1 and R2). The refractive index measures how much light bends when passing through a material, while the radii of curvature describe the two curved surfaces of the lens.

By manipulating these parameters, lensmakers can design lenses with specific focal lengths to meet various optical needs. For instance, a lens with a shorter focal length will focus light more strongly, resulting in a larger, magnified image.

Practical Applications of Lens Equations

Lens equations have widespread applications in fields like photography, ophthalmology, and astronomy. In photography, they determine the appropriate lens settings for capturing sharp images. In ophthalmology, they help design corrective lenses for vision impairments. And in astronomy, they are used to calculate the focal lengths of telescopes, enabling us to explore the distant reaches of the cosmos.

Understanding the thin lens equation and the lensmaker’s equation is fundamental to comprehending the behavior of lenses and their applications in various domains. These equations empower us to manipulate light, create clear images, and unlock the secrets of the universe.