How To Calculate Density Of A Cylinder With Simple Measurements
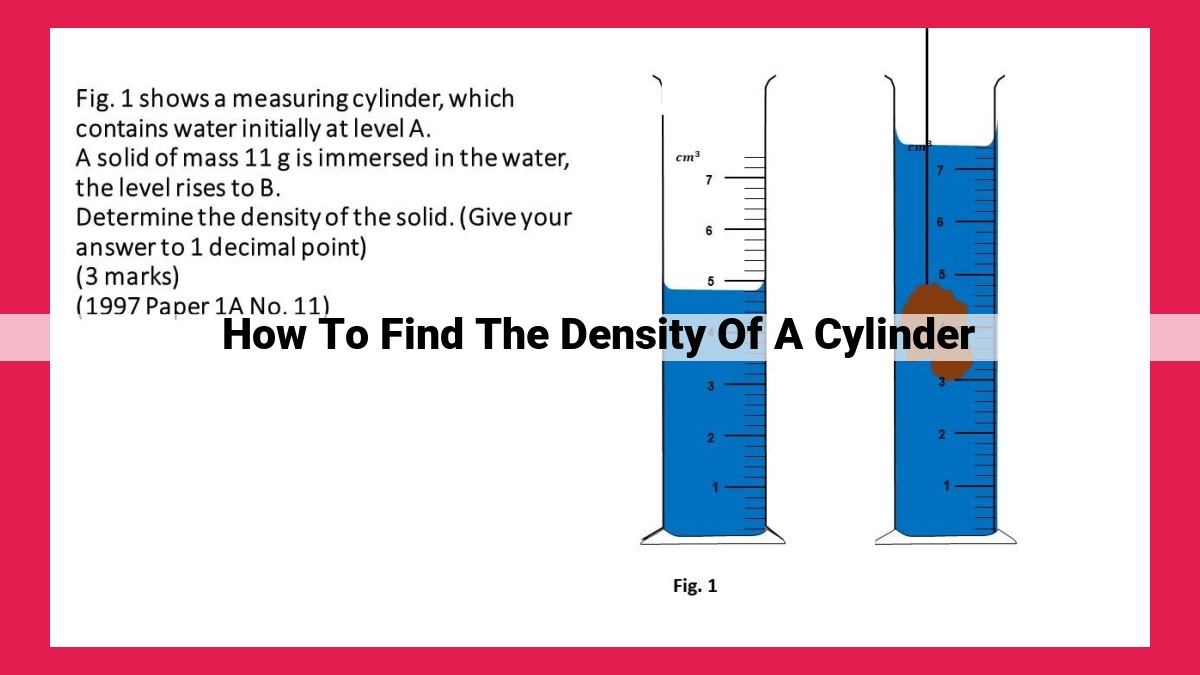
To find the density of a cylinder, measure its mass (M) using a scale. Determine the radius (r) and height (h) using a ruler. Calculate the volume (V) using the formula V = πr²h. Finally, divide the mass by the volume: Density = M / V. This formula provides the density in units of mass per unit volume, such as grams per cubic centimeter (g/cm³). The density represents the compactness of the material, indicating how much mass is packed into a given volume.
Unveiling the Secrets of Density: A Matter of Mass and Volume
In the realm of science, density stands as a pivotal concept, providing us with a profound understanding of matter’s intricate properties. Density, the mass per unit volume, unveils the essence of substances, empowering us to unravel their secrets and navigate the world around us.
Whether it’s the buoyancy of a ship gliding across the vast oceans or the purity analysis of valuable materials, density plays a crucial role in shaping our everyday lives. By understanding the intricacies of density, we unlock the ability to decipher the mysteries of our physical world.
The Importance of Density
Imagine a world without density: a chaotic realm where objects float aimlessly, their mass and volume bearing no significance. It would be a puzzling and unpredictable existence, where buoyancy and the properties of substances would be enigmatic.
Density, however, brings order to this chaos, providing a tangible measure of matter’s compactness. It allows us to distinguish between materials, comprehend their behavior in various environments, and make informed decisions about their use in different applications. In essence, density is the cornerstone of understanding the physical properties of matter.
Fundamental Concepts Underlying Density
When studying matter, density plays a crucial role in understanding its properties and behavior. To fully grasp this concept, we need to explore the fundamental building blocks of mass, volume, and their interplay in determining density.
Mass:
Mass represents the quantity of matter contained within an object. It’s an invariant property, meaning it remains the same regardless of the object’s location or movement. Mass can be measured using various instruments, such as scales or balances.
Mass is closely related to other physical quantities like weight, inertia, and momentum. Weight is the force exerted on an object due to gravity and varies depending on the gravitational field it experiences. Inertia refers to an object’s resistance to changes in its motion, which is directly proportional to its mass. Momentum is the product of mass and velocity, and it represents the amount of motion an object possesses.
Volume:
Volume describes the amount of space occupied by an object. It can be measured in various units, commonly represented in cubic units like cubic centimeters (cm³) or cubic meters (m³). Volume is related to concepts like capacity, which describes how much fluid a container can hold, and displacement, the amount of fluid displaced by an immersed object.
Density:
Density is a measure of how tightly packed matter is within a substance. It’s defined as the mass of a material per unit volume. Density is expressed in units such as grams per cubic centimeter (g/cm³) or kilograms per cubic meter (kg/m³).
Density is a crucial factor in understanding how substances behave. It’s related to specific gravity, which compares the density of a substance to the density of water. Buoyancy is another phenomenon influenced by density; objects with lower density tend to float in fluids with higher density. Additionally, density plays a role in determining a substance’s compressibility, or its ability to be compressed under pressure.
Essential Measurements for Cylinders
Imagine yourself as a budding scientist embarking on a thrilling journey to unravel the enigmatic world of density. As you navigate through this uncharted territory, you’ll encounter the need to measure the essential dimensions of cylinders. Let’s delve into the fascinating details of these measurements:
Radius: The Heart of the Circle
The radius of a cylinder, like the spoke of a wheel extending from its center to the edge, defines its circular boundaries. It’s intimately related to other essential measurements like the diameter, which is the distance across the circle, and the circumference, the total length of its perimeter.
Height: Reaching for the Sky
The height of a cylinder, like a skyscraper piercing the clouds, measures the vertical distance from its base to its top. It’s often referred to as the length or altitude of the cylinder and plays a crucial role in determining its volume.
Pi (π): The Mathematical Constant
In the realm of circles, spheres, and cylinders, a special mathematical constant emerges: π (pi). This enigmatic number, approximately equal to 3.14, serves as the ratio of a circle’s circumference to its diameter. Its presence is indispensable in calculating the volume of a cylinder, guiding us towards precise and accurate results.
Calculating the Density of a Cylinder: An In-depth Exploration
Understanding Density
The density of an object measures how tightly packed its matter is. It’s an essential property for understanding a substance’s behavior, such as its buoyancy and compressibility.
Fundamental Concepts
- Mass: A measure of an object’s matter content. It’s related to weight, inertia, and momentum.
- Volume: The amount of three-dimensional space an object occupies.
- Density: Mass per unit volume. It’s directly proportional to mass and inversely proportional to volume.
Essential Measurements for Cylinders
To calculate the density of a cylinder, we need to measure its radius (r) and height (h). The radius is the distance from the center of the circular base to its edge, while the height is the distance from the base to the top.
Deriving the Formula
The volume of a cylinder can be calculated using the formula: V = πr²h
where π (pi) is a mathematical constant approximately equal to 3.14.
Substituting this formula into the density equation, we get:
Density = Mass / Volume
Density = Mass / (πr²h)
Applying the Formula
This formula allows us to determine the density of a cylinder given its mass and dimensions. By measuring the mass using a scale and the radius and height using a ruler or measuring tape, we can calculate the density using the formula.
Understanding the concept of density is vital for studying matter and its properties. By applying the density formula specifically designed for cylinders, we can easily determine the density of cylindrical objects, enabling us to analyze and compare different substances. This knowledge finds applications in various fields, including engineering, materials science, and chemistry.
Applications of Density in Practice
Understanding the concept of density is crucial in various fields of science and engineering. Its practical applications extend beyond theoretical calculations, providing valuable insights into the properties and behavior of matter. Here are some key areas where density plays a significant role:
Buoyancy Determination
Density is essential in determining the buoyancy of objects immersed in fluids. According to the Archimedes principle, an object submerged in a fluid experiences an upward buoyant force equal to the weight of the fluid displaced by the object. By knowing the density of both the object and the fluid, we can predict whether an object will float, sink, or remain suspended. This principle is utilized in designing ships, submarines, and other marine vessels, ensuring their stability and buoyancy.
Material Purity Measurement
Density is also a critical factor in measuring the purity of materials. Different substances exhibit distinct densities, and any variation from the expected value can indicate impurities or adulteration. For example, in the pharmaceutical industry, the density of a drug sample can reveal the presence of inactive ingredients or contaminants, ensuring the quality and efficacy of the product.
Substance Classification
Scientists and engineers classify substances based on their densities. This classification helps identify and characterize different materials, as well as predict their behavior in various applications. For instance, in geology, the density of rocks and minerals can provide clues about their composition, origin, and geological processes. This information assists in exploration, resource management, and understanding Earth’s history.
By delving into these practical applications, we recognize the importance of density in shaping our understanding of the physical world around us. It empowers scientists, engineers, and researchers with the ability to analyze, predict, and manipulate the behavior of matter for countless technological advancements and scientific discoveries.