Calculate Average Velocity From Velocity-Time Graphs: A Step-By-Step Guide
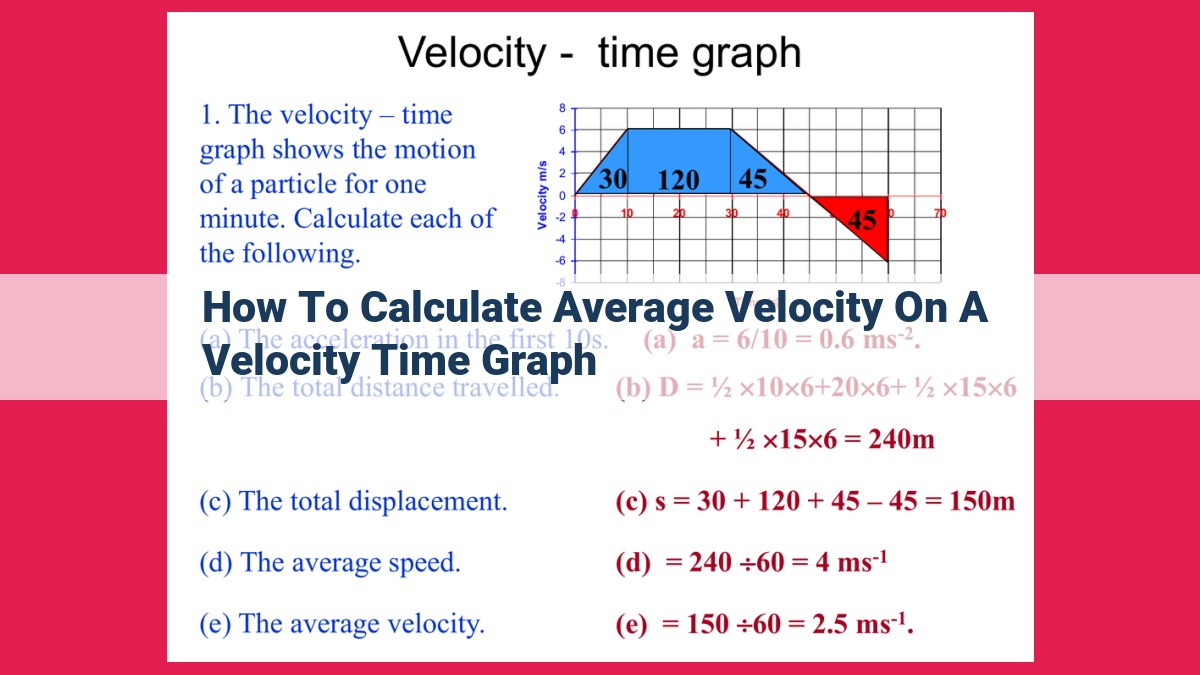
To calculate average velocity on a velocity-time graph, first identify a time interval. Then, measure the change in velocity (rise) and the change in time (run). Calculate the slope of the line segment formed by these points. The slope represents the average velocity, which is the displacement (change in position) divided by the time interval. This calculation allows you to determine the overall speed and direction of an object over a specific time period.
Unveiling the Secrets of Velocity-Time Graphs
In the realm of physics, graphs serve as invaluable tools to unravel the mysteries of motion. Among these graphs, velocity-time graphs hold a special place, offering a window into the intricacies of an object’s velocity over time. This blog post embarks on a journey to demystify these graphs, guiding you step-by-step through the process of calculating average velocity on a velocity-time graph.
The Essence of Velocity-Time Graphs
Velocity-time graphs are essentially pictorial representations of an object’s velocity as it varies over time. They consist of a horizontal axis representing time and a vertical axis representing velocity. By plotting points on this graph, we create a visual depiction of the object’s motion and can discern important information about its velocity.
One of the most crucial concepts in understanding these graphs is slope. Slope, represented by the rise over run, indicates an object’s acceleration. In the context of a velocity-time graph, the rise refers to the change in velocity, while the run refers to the corresponding change in time.
Comprehending slope is fundamental because it provides a direct way to determine an object’s average velocity over a specific time interval. Average velocity is simply the rate of change in an object’s position, and it can be calculated using the formula:
Average velocity = Displacement ÷ Time
Breaking Down the Calculation Process
Now, let’s delve into the step-by-step guide to calculating average velocity on a velocity-time graph:
- Identify the time interval over which you want to calculate average velocity.
- Determine the rise (change in velocity) and run (change in time) within the selected interval.
- Calculate the slope by dividing the rise by the run. Remember, slope represents the average velocity.
- Interpret the slope as the object’s average velocity over the given time interval.
By skillfully applying these steps, you can unlock the secrets of velocity-time graphs and gain valuable insights into an object’s motion.
Understanding Velocity-Time Graphs
Velocity-time graphs are visual representations of how an object’s velocity changes over time. They plot velocity on the y-axis and time on the x-axis. Each point on the graph represents the object’s velocity at a specific time.
The slope of a velocity-time graph is a crucial concept to understand. Slope measures the rate of change in velocity. A positive slope indicates that the object is accelerating, while a negative slope indicates that it is decelerating. A slope of zero means the object is moving at a constant velocity.
By interpreting the slope of a velocity-time graph, we can gain valuable insights into an object’s motion. For instance, a steep positive slope indicates rapid acceleration, while a shallow positive slope suggests a more gradual change in velocity. Similarly, a steep negative slope corresponds to rapid deceleration, while a gentle negative slope represents a more moderate change in velocity.
Calculating Rise and Run
- Define rise as the change in velocity and run as the change in time.
- Explain how to identify these values on a velocity-time graph.
Decoding Velocity-Time Graphs: Unlocking the Secrets of Rise and Run
Imagine embarking on a journey to decipher the mysteries of velocity-time graphs. In this adventure, we’ll uncover the pivotal concepts of rise and run, the essential building blocks for calculating average velocity.
A velocity-time graph is a visual representation of an object’s velocity over a specific time interval. Velocity, measured in meters per second (m/s), describes how fast an object is moving. Time, measured in seconds (s), captures the duration of an object’s motion.
On a velocity-time graph, the rise refers to the change in velocity. It measures the vertical distance between two points on the graph, representing the amount by which velocity has increased or decreased.
The run, on the other hand, represents the change in time. It measures the horizontal distance between the same two points, indicating the duration of the velocity change.
To identify the rise and run on a velocity-time graph, simply select two points along the line segment representing the object’s motion. The vertical distance between these points gives you the rise, while the horizontal distance gives you the run.
Armed with these newfound insights, we’re ready to embark on the thrilling quest of calculating average velocity from velocity-time graphs. Stay tuned for the next chapter of our adventure, where we’ll dive into the intricacies of the average velocity equation!
Average Velocity Equation
- Introduce the equation for average velocity: Average velocity = Displacement / Time.
- Explain that displacement is not shown on a velocity-time graph.
Understanding the Average Velocity Equation
When calculating average velocity on a velocity-time graph, we rely on the equation Average Velocity = Displacement / Time. However, displacement is not directly represented on a velocity-time graph. So, how do we make sense of this equation?
The crux of this challenge lies in the fact that velocity is the rate of change of displacement. In other words, if we know the velocity at every instant of time over a given interval, we can reconstruct the total displacement during that interval.
Interpreting the Equation
The equation Average Velocity = Displacement / Time can be interpreted as follows:
- Average velocity is a single numerical value that represents the rate at which an object moves over a specific time interval.
- Displacement is the total distance an object moves in a specified direction, from its starting point to its ending point.
- Time is the duration of the time interval over which the average velocity is calculated.
Overcoming the Graph’s Limitation
Since a velocity-time graph does not directly display displacement, we must rely on alternative methods to determine this value. One common approach is to use the concept of area under a curve.
The area under the velocity-time graph between two points represents the total displacement of the object over the corresponding time interval. By calculating this area, we can effectively obtain the displacement values needed to apply the average velocity equation.
A Comprehensive Guide to Calculating Average Velocity on a Velocity-Time Graph
Understanding the Essence of a Velocity-Time Graph
A velocity-time graph is a graphical representation of an object’s velocity (speed and direction) over time. It allows us to visualize the changes in an object’s motion. The slope of the graph, known as the slope, represents the average velocity of the object during a specific time interval.
Determining Rise and Run: The Key Values
To calculate average velocity, we need to determine the rise and run of the velocity-time graph within a particular time interval. Rise is the difference in velocity, while run is the difference in time.
Step-by-Step Guide: Unraveling the Average Velocity Formula
Once we have identified the time interval, rise, and run, we can calculate the average velocity using the following steps:
-
Calculate Slope: Divide the rise (change in velocity) by the run (change in time).
-
Interpret Slope: The slope, which is a constant value, represents the object’s average velocity during that time interval.
Examples and Applications: Exploring Real-World Scenarios
Let’s consider a scenario where a car travels at a constant velocity of 60 km/h for 1 hour. The velocity-time graph will be a straight line with a slope of 60 km/h. This slope represents the car’s constant average velocity of 60 km/h.
Another example is a ball thrown vertically upward. The velocity-time graph will be a parabola. The slope of the upward portion of the graph represents the initial velocity of the ball, while the negative slope of the downward portion represents the final velocity (just before it hits the ground).
Examples and Applications of Average Velocity Calculations on Velocity-Time Graphs
Grasping the Concept through Examples
To solidify your understanding, let’s delve into some examples. Imagine a velocity-time graph representing a car’s motion over time. The graph shows a constant velocity line, indicating that the car is moving at a steady speed. To calculate the average velocity, simply identify the horizontal time interval and measure the vertical change in velocity. The slope of this line represents the average velocity of the car over that specific time interval.
Real-World Applications: From Sports to Physics
Calculating average velocity extends beyond theoretical exercises and finds practical applications in various fields. In the realm of sports, it’s used to determine an athlete’s average speed during a race. By measuring the distance covered and the time taken, coaches and analysts can assess the athlete’s performance and identify areas for improvement.
Similarly, in physics, calculating average velocity plays a crucial role in solving motion-related problems. For instance, it’s used to determine the average speed of an object moving with non-uniform acceleration. By analyzing velocity-time graphs, physicists can gain insights into the motion of objects and make predictions about their future trajectories.
Practical Examples: Bringing the Concept to Life
To further illustrate, consider the following scenario: You’re tasked with calculating the average velocity of a runner during a 100-meter dash. Armed with a velocity-time graph, you measure the horizontal time interval to be 10 seconds and the vertical change in velocity to be 10 meters per second. Using the formula, you calculate the average velocity to be 1 meter per second, indicating the runner’s steady pace throughout the race.
In another example, let’s say you’re analyzing the motion of a ball thrown into the air. The velocity-time graph reveals an upward trajectory followed by a downward trajectory. By calculating the average velocity during the upward motion, you can determine the initial upward velocity of the ball. Similarly, by calculating the average velocity during the downward motion, you can estimate the final downward velocity just before the ball hits the ground.
Calculating average velocity on velocity-time graphs is a versatile skill with applications in both academic and real-world scenarios. By grasping the concepts and practicing with examples, you can confidently navigate problems involving motion and velocity, gaining a deeper understanding of the physical world around you.