Understanding The Bell-Shaped Histogram: Unraveling Normal Data Distribution

The histogram exhibits a distinct shape characterized by a bell-shaped curve. This symmetrical distribution indicates a normal distribution, with data points clustered around the mean. The curve is evenly distributed on both sides of the mean, with no significant skewness or kurtosis. Such histograms represent data that follows a Gaussian or normal distribution, commonly found in natural phenomena and statistical processes.

• Definition and purpose of a histogram
• How histograms visually represent data

Understanding Histograms: A Visual Guide to Data Analysis

Histograms are not just graphs—they’re storytelling tools that unveil the hidden patterns within your data. Definitionally, a histogram is a graphical representation that visually displays the frequency distribution of a dataset. It’s like a snapshot of your data, capturing the number of observations that fall within specific value ranges. Each bar in a histogram represents a particular range of values, and the height of the bar corresponds to the number of observations in that range.

Now, let’s simplify this: Imagine you want to analyze the heights of students in your class. You could jot down each student’s height and sort the values to see how they stack up. But a histogram is more intuitive. It paints a visual picture, making it easy to spot patterns and trends. The vertical axis shows the frequency (how many students) for each interval (height range) on the horizontal axis. You’ll instantly see the mean (average height), mode (most common height), and median (middle height) just by looking at the shape of the histogram.

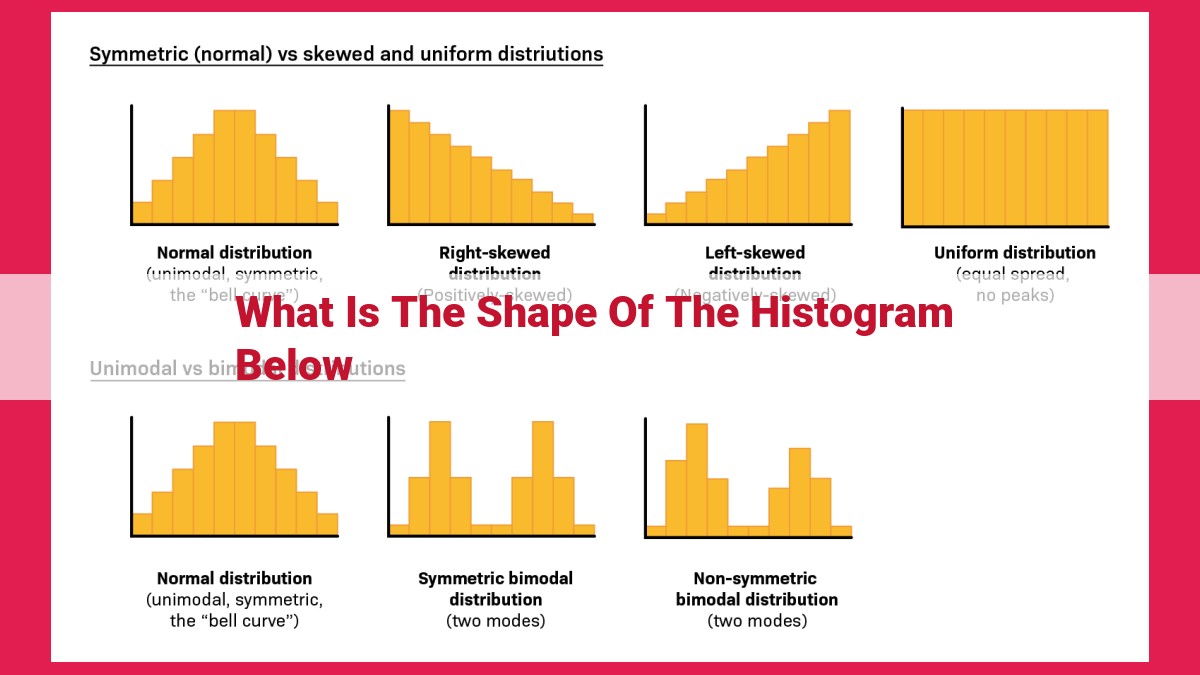
Types of Histogram Shapes

• Overview of common histogram shapes
• Importance of understanding shape for data analysis

Types of Histogram Shapes

Overview

Histograms are graphical representations of data, revealing patterns and distributions in a visually accessible manner. Understanding the various shapes histograms can take is crucial for effective data analysis.

Importance of Shape

The shape of a histogram provides valuable insights into the underlying data. It can reveal:

• Central tendency (mean, median)
• Dispersion (standard deviation)
• Skewness (asymmetry)
• Multimodality (multiple peaks)
• Outliers (extreme values)

By interpreting histogram shapes, we can gain a deeper understanding of the nature of data and make informed conclusions.

Common Histogram Shapes

Symmetric (Bell-Shaped)

When data is evenly distributed around the mean, the histogram takes a symmetric, bell-shaped form. This indicates a normal distribution and implies that most values fall close to the average.

Skewed

Skewness refers to the asymmetry in a histogram.

• Positive skew: Data is shifted to the left, with a longer tail on the right.
• Negative skew: Data is shifted to the right, with a longer tail on the left.

Skewness provides information about the distribution of values relative to the mean.

Uniform

A uniform histogram appears as a flat line. This indicates that all values are equally represented, with no significant central tendency or dispersion.

Multimodal

Multimodal histograms have multiple peaks, reflecting the presence of two or more distinct groups or patterns within the data.

Bimodal

A bimodal histogram has two distinct peaks. This suggests the presence of two separate populations or data sets with different characteristics.

The shape of a histogram is an invaluable tool for understanding data distributions and patterns. By recognizing and interpreting common histogram shapes, analysts can effectively extract insights, make informed decisions, and communicate data findings effectively.

Symmetric Histogram (Bell-Shaped)

• Characteristics and properties of symmetric histograms
• Significance of normal distributions

Symmetric Histograms: A Tale of Perfect Balance

In the realm of data visualization, histograms are like superheroes, revealing hidden patterns within numerical datasets. Among the spectrum of histogram shapes, symmetric histograms stand out as a beacon of balance and harmony.

Symmetric histograms resemble the iconic bell curve, gracefully arching from the center to both sides. This symmetry reflects a normal distribution—a statistical phenomenon where data points are evenly spread around the mean, or average value.

Like an undisturbed lake, normal distributions represent a remarkable symmetry. The data points to the left and right of the mean mirror each other, creating a perfect equilibrium. This shape implies that extreme values are rare, with most data points clustering around the center.

Significance of Normal Distributions

Normal distributions are not just mathematical abstractions; they are fundamentally intertwined with natural phenomena. Many real-world processes, from human heights to exam scores, exhibit normal distributions.

In statistics, normal distributions are considered a gold standard. They provide a baseline for comparison, allowing us to identify deviations from the norm. This understanding is crucial in fields such as quality control, where Abweichungen can signal potential issues.

Moreover, normal distributions enable us to make predictions about future outcomes. Knowing that data follows a normal distribution, we can estimate the likelihood of specific values occurring within a given range. This knowledge empowers us to make informed decisions based on data patterns.

Key Takeaway

Symmetric histograms, with their telltale bell curve and normal distribution, paint a picture of balance and uniformity. They are invaluable tools for understanding data patterns, identifying potential issues, and making predictions. As we delve into the world of data visualization, let us embrace the power of symmetric histograms—a testament to the hidden harmonies within our numerical world.

Skewed Histograms: Unraveling the Secrets of Asymmetric Data

When data distributions deviate from the comforting symmetry of a bell-shaped curve, they reveal themselves as skewed histograms, captivating tales of unequal and captivating data patterns. In the realm of histograms, skew holds the key to unlocking the intricacies of such distributions, guiding us through the nuances of their characteristics and their profound implications for data interpretation.

Negative Skew: A Tale of Left-Leaning Data

Negative skew, like an unyielding force, pulls the histogram’s peak towards the right-hand side of the graph. It whispers a story of outliers dwelling on the higher end of the spectrum, creating a long, trailing tail extending to the left. This asymmetrical canvas paints a picture of data clumped closer to the lower end, leaving behind a sparse scattering of values towards the higher end.

Positive Skew: Embracing the Right-Hand Side

Positive skew, the mirror image of its negative companion, paints a captivating contrast. Here, the histogram’s peak gracefully leans to the left, mirroring the presence of outliers congregating at the lower end. Its distinct silhouette boasts a long, trailing tail stretching to the right, evoking a visual symphony of data points clustered towards the higher end.

Interpreting Skewness: Unveiling the Hidden Story

Skewness offers a profound window into data distributions, unraveling their hidden stories. Negative skew suggests that most values tend to be lower than the mean, while positive skew whispers the opposite – most values reside above the mean. This asymmetry provides invaluable insights into the underlying processes that have shaped the data, revealing trends and patterns that might otherwise remain hidden.

Applications of Skewness: From Research to Real-World Insights

The utility of skewness extends far beyond the theoretical realm, reaching into diverse fields. In finance for instance, positive skew in stock returns may signal potential for higher returns, while negative skew could indicate increased volatility. Medical research leverages skewness to analyze health data, identifying skewed distributions that may point to underlying health conditions or treatment outcomes.

In the bustling world of business analytics, skewed histograms provide a roadmap for understanding customer behavior. Skewness in sales data may reveal concentration in specific product categories, guiding marketing strategies and inventory management. Even in the realm of social science, skewness unveils the nuances of human behavior, shedding light on patterns in income distribution or political preferences.

Uniform Histogram: Unveiling the Absence of a Preferred Value

In the realm of histograms, a uniform distribution stands apart with its distinctive flat shape. Unlike the bell-shaped curves, bimodal peaks, or skewed slopes of other histograms, a uniform distribution resembles a straight line, indicating a lack of a preferred value.

This uniform spread suggests that all values within the data set are equally likely to occur. There is no central tendency, no outliers, and no discernible patterns. The histogram resembles a flat, featureless landscape, with each data point contributing equally to the overall distribution.

Uniform distributions are often encountered in scenarios where randomness reigns supreme. For instance, if you were to randomly select integers between 1 and 100, the resulting histogram would likely exhibit a uniform shape. This is because each integer has an equal chance of being chosen, and there is no inherent bias towards any particular value.

Another implication of a uniform distribution is that the mean, median, and mode are all equal. This is because the data is evenly spread out, and there is no single value that occurs more frequently than others.

In summary, a uniform histogram signifies the absence of any discernible patterns or trends. It suggests that all values within the data set are equally likely to occur, and that there is no preferred or typical value. This type of distribution is often found in situations involving randomness or a deliberate effort to create a uniform distribution, such as in random sampling or lottery draws.

Multimodal Histograms: Unveiling Complex Data Patterns

Imagine a group of students taking a test. After grading the papers, the teacher wants to visualize the distribution of scores. A histogram is a powerful tool for this task, and in this case, it reveals an intriguing pattern: a multimodal histogram.

Understanding Multimodal Distributions

A multimodal histogram is one that exhibits multiple peaks, indicating the presence of several distinct groups or clusters within the data. Unlike unimodal histograms with a single peak, these histograms suggest a more complex underlying structure.

Causes of Multimodal Data

Multimodal distributions can arise due to various reasons. One common cause is the presence of multiple sources or populations within the data. For instance, if a dataset includes exam scores from different classes or sections, it might exhibit multiple peaks, each representing the distribution of scores within a specific group.

Dealing with Data with Multiple Modes

Understanding multimodal histograms requires careful consideration. Researchers and data analysts must determine whether the multiple modes represent meaningful subgroups or simply random fluctuations. Data exploration techniques, such as clustering and subspace analysis, can help identify the underlying structure.

In some cases, it may be necessary to separate the data into multiple groups or subsets to analyze each mode independently. This approach allows for a more refined understanding of the data’s characteristics within each subgroup.

Multimodal histograms provide valuable insights into complex datasets, highlighting the presence of multiple modes or distinct groups. By understanding the causes and implications of these distributions, researchers can gain a deeper understanding of their data, leading to more informed decision-making and analysis.

Bimodal Histograms: Uncovering the Tale of Two Peaks

In the realm of statistics, when it comes to visualizing data, histograms take center stage. These graphical representations unravel the hidden patterns within numerical information, revealing the shape of the distribution. Among the diverse histogram shapes, the bimodal histogram stands out with its unique characteristics and intriguing implications.

What is a Bimodal Histogram?

A bimodal histogram, as its name suggests, is characterized by two distinct peaks. These peaks represent two dominant values or groups within the data. Unlike other histograms, bimodal distributions display a clear separation between these two peaks, indicating the presence of two distinct subpopulations or variables.

Interpretation of Bimodal Distributions

The presence of two peaks in a bimodal histogram suggests a non-random pattern in the data. It often occurs when there are two distinct sets of observations with different underlying causes. For instance, a bimodal histogram of test scores might indicate the presence of two separate classes within a school, each with its unique academic performance.

Practical Applications

Bimodal histograms find applications in various fields, including:

• Social Sciences: Analyzing survey data with different response categories.
• Biology: Representing the distribution of species abundance in different habitats.
• Economics: Studying income distributions with concentrations at different income levels.

Understanding Bimodal Histograms

To fully grasp the significance of bimodal histograms, it’s crucial to understand the concept of multiple modes. Mode refers to the value that occurs most frequently in a distribution. In a bimodal histogram, there are two distinct modes, each representing a peak in the distribution.

The interpretation of bimodal histograms depends on the context of the data. Sometimes, they may indicate a mixture of two different populations, each with its statistical characteristics. In other cases, they might suggest an underlying bimodal process, such as a periodic function or a distribution with two independent factors.

When encountering a bimodal histogram, it’s essential to explore the underlying causes and investigate the factors that contribute to the two peaks. This understanding empowers researchers and analysts to uncover deeper insights and make informed decisions based on the data they possess.

The Significance of Histogram Shape

In the realm of data analysis, histograms emerge as indispensable tools, providing a visual representation of data distribution. Delving into the shape of a histogram unlocks a treasure trove of insights, revealing patterns and trends within the data.

Unveiling Data Patterns

The contours of a histogram paint a vivid picture of the underlying data. A bell-shaped histogram, for instance, suggests a normal distribution, where most data points cluster around the mean. Understanding this shape enables data scientists to make informed inferences about the likelihood of certain outcomes.

In contrast, skewed histograms, with their lopsided appearance, indicate an uneven distribution. Negative skew implies a longer tail of data points towards smaller values, while positive skew suggests a greater concentration of data points towards larger values. These shapes provide valuable insights into data outliers and the presence of extreme values.

Empowering Data Analysis and Research

The shape of a histogram plays a pivotal role in data analysis and research. By examining histogram shapes, researchers can identify deviations from normality, discover multimodal distributions indicating multiple distinct groups within the data, and uncover bimodal distributions suggestive of two distinct populations or variables.

Understanding histogram shapes allows researchers to draw meaningful conclusions, make accurate predictions, and test hypotheses with greater confidence. In fields such as statistics, finance, and healthcare, histogram analysis has become an indispensable tool for extracting valuable insights from complex data.

Applications of Histogram Shapes: Unlocking Data Insights

Histograms, with their distinct shapes, offer a powerful window into the patterns and characteristics of data. They serve as valuable tools in a wide range of fields, providing crucial insights that drive informed decision-making.

Statistics and Data Analysis

In the realm of statistics, histograms play a critical role. They can uncover hidden trends, identify outliers, and reveal underlying distributions within data. By analyzing the shape of a histogram, researchers can gain valuable insights into the distribution of data points, the presence of skewness or kurtosis, and the overall normality of a dataset. This information is invaluable for drawing accurate conclusions and making evidence-based inferences.

Healthcare and Medical Research

Histograms have found significant applications in healthcare and medical research. They can be used to visually represent patient data, such as age, height, weight, or test results. By identifying patterns in these histograms, medical professionals can spot correlations, detect anomalies, and make informed diagnoses. Moreover, histograms can assist in drug development, treatment optimization, and epidemiological studies.

Marketing and Business Analysis

In the world of marketing and business analysis, histograms provide valuable insights into consumer behavior, market trends, and sales patterns. By analyzing the shape and characteristics of histograms, marketers can segment customer bases, identify target audiences, and develop tailored marketing strategies. Additionally, histograms can be used to analyze sales data, forecast demand, and optimize inventory management.

Education and Research

Histograms have also found their way into education and research environments. In educational settings, they can be used to represent student performance, track progress, and identify areas for improvement. In scientific research, histograms are used to analyze experimental data, compare results, and draw conclusions. The ability of histograms to convey complex information in a digestible format makes them an essential tool for researchers across various disciplines.

In conclusion, the shape of a histogram offers a wealth of insights that can be applied to diverse fields. From statistics and data analysis to healthcare, marketing, education, and research, histograms serve as powerful visualization tools that uncover hidden patterns, facilitate informed decisions, and drive innovation.