Calculating Average Velocity From A Velocity-Time Graph: A Comprehensive Guide For Motion Analysis

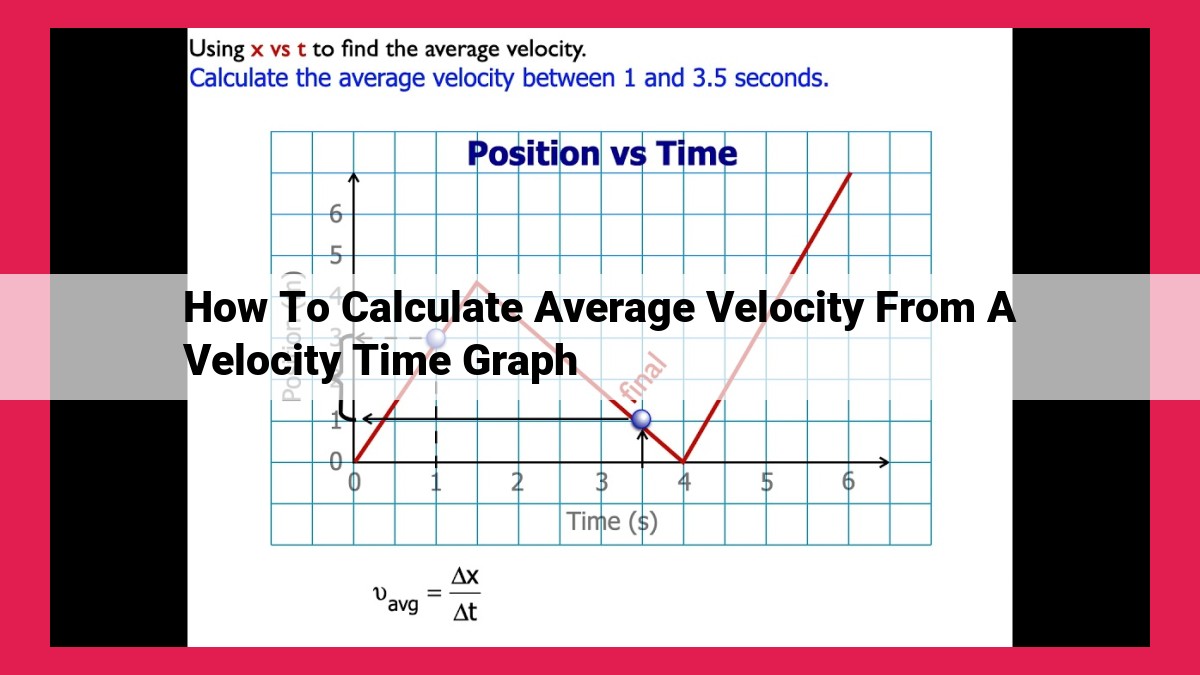
To calculate average velocity from a velocity-time graph, determine the object’s displacement by subtracting the initial and final positions. Then, divide this displacement by the total time elapsed to find the average velocity. A positive slope on the graph indicates motion in the positive direction, while a negative slope indicates motion in the negative direction. The slope of the line represents the velocity of the object, making it easy to determine the velocity at any point in time. This method provides a convenient way to calculate the average velocity of objects in various motion scenarios, aiding in the analysis and interpretation of their movement.

Grasping Average Velocity: A Journey of Motion

Imagine you’re in a race, sprinting towards the finish line. The distance you cover in a certain amount of time determines how fast you’re running, right? That’s exactly what average velocity is all about. It tells us how swiftly an object moves over a specific time interval.

Understanding average velocity is crucial for describing an object’s motion. It’s like a snapshot that captures how far and how quickly an object has moved in a given time frame. This information is essential in various fields, such as engineering, physics, and even everyday life. So, let’s dive deeper into the world of average velocity and unveil its secrets.

Interpreting a Velocity-Time Graph

In the realm of motion analysis, velocity-time graphs serve as invaluable tools, offering a visual representation of an object’s journey through space and time. By skillfully deciphering these graphs, we unlock a treasure trove of information about an object’s displacement, time of travel, and velocity.

Identifying Displacement

The displacement, or change in position, can be determined by examining the vertical axis of the graph, which displays the object’s velocity. To calculate displacement, simply subtract the initial position from the final position along the vertical axis.

Time Elapsed

The time elapsed during the object’s motion is represented by the horizontal axis of the velocity-time graph. By analyzing the interval between the initial time and the final time, we can determine the total duration of the object’s journey.

Velocity

The velocity, or rate of change in position, is the slope of the line on the velocity-time graph. By calculating the slope using the formula (Δy/Δx), we can determine the object’s velocity at any given point in time. A positive slope indicates an increase in velocity, while a negative slope indicates a decrease in velocity.

Visualizing the Object’s Motion

Imagine a car traveling on a highway. Its velocity-time graph would resemble a straight line with a positive slope, indicating that the car is accelerating. On the other hand, if the car were braking, the graph would display a straight line with a negative slope.

Practical Applications

Velocity-time graphs find widespread use in various fields. For instance, they can help us calculate the distance traveled by a car over a certain period or determine the projectile’s velocity at a specific instant. By harnessing the power of these graphs, we gain invaluable insights into the dynamics of moving objects.

Calculating Displacement from a Velocity-Time Graph: A Step-by-Step Guide

Understanding the displacement of an object from its velocity-time graph is crucial for analyzing its motion. Displacement represents the change in position of an object over a given time interval. To determine displacement from a velocity-time graph, it involves identifying the initial and final positions of the object and calculating the difference between them.

First, identify the time at which the object starts and the time at which it stops on the time axis of the graph. These points represent the initial and final positions of the object. Next, locate the corresponding vertical lines on the velocity axis that intersect with these time points. The intersections of these lines with the velocity axis represent the initial and final velocities of the object.

To calculate the displacement, simply subtract the initial position from the final position. The result will provide you with the magnitude of the displacement, which represents the total distance covered by the object while moving from its initial to its final position. It’s important to note that displacement can be either positive or negative:

• Positive displacement indicates that the object has moved in the positive direction of the chosen axis.
• Negative displacement suggests movement in the negative direction.

Remember, the displacement calculated from a velocity-time graph is a scalar quantity, meaning it only describes the magnitude of the displacement, not its direction. To obtain the complete description of the object’s motion, the displacement should be considered in conjunction with its velocity.

Calculating Average Velocity from the Graph

To calculate the average velocity of an object from a velocity-time graph, we need to determine its displacement and total time.

Displacement is the change in the object’s position over time. On a velocity-time graph, displacement is represented by the area between the line and the time axis. To find the displacement, we subtract the initial position from the final position.

Total time is the total duration of the object’s motion. On a velocity-time graph, it is represented by the horizontal length of the line.

Once we have the displacement and total time, we can calculate the average velocity using the formula:

Average Velocity = Displacement / Total Time

The average velocity tells us how fast and in which direction the object is moving over the entire time interval.

Example:

Consider a velocity-time graph where the object starts at a position of 5m and moves with a constant velocity of 10m/s for 2 seconds. The graph is a straight line with a slope of 10m/s.

• Displacement: 10m (final position – initial position)
• Total Time: 2s
• Average Velocity: 10m / 2s = 5m/s

This means the object moved with an average velocity of 5m/s for 2 seconds, indicating a uniform motion.

In summary, calculating average velocity from a velocity-time graph involves determining the displacement and total time represented by the graph. The average velocity is then calculated as the displacement divided by the total time. This value provides critical information about the object’s motion, including its speed and direction.

Slope and Velocity: Unraveling the Connection

In the realm of motion, velocity plays a pivotal role in describing an object’s journey. Analyzing a velocity-time graph unveils a wealth of information about the object’s speed and direction. One crucial aspect of this graph is the slope of the line. It holds the key to unlocking the object’s velocity.

Imagine a velocity-time graph as a pictorial representation of an object’s motion. The horizontal axis measures time, while the vertical axis measures velocity. The slope of a line on this graph, calculated as the change in velocity divided by the change in time, reveals the object’s average velocity.

Positive Slope, Positive Velocity:

When the slope is positive, the line on the graph ascends. This indicates that the object’s velocity is increasing. As time progresses, the object is moving faster and faster.

Negative Slope, Negative Velocity:

Conversely, a negative slope signifies a descending line on the graph. This suggests that the object’s velocity is decreasing. Over time, the object is slowing down.

Zero Slope, Constant Velocity:

A zero slope corresponds to a horizontal line on the graph. This indicates that the object’s velocity is constant. It is moving at a steady pace, neither accelerating nor decelerating.

Slope and Direction:

In addition to magnitude, the slope also provides insight into the direction of the object’s motion. A positive slope implies that the object is moving in a positive direction, while a negative slope indicates movement in a negative direction.

By understanding the relationship between the slope and velocity, we gain a deeper comprehension of an object’s motion. This knowledge empowers us to analyze graphs, calculate average velocities, and describe the dynamics of real-world objects, from the motion of a pedestrian to the trajectory of a projectile.

Positive and Negative Velocity: The Tale of Direction

Velocity, the vector quantity representing both speed and direction, plays a crucial role in understanding an object’s motion. When we talk about velocity, it’s not just about how fast something is moving but also which way it’s headed. This directionality is elegantly captured in velocity-time graphs, where the slope of the line tells us all we need to know.

A positive slope indicates an upward slant, signifying that the object’s velocity is increasing in a positive direction. This means the object is either moving faster in the same direction or decelerating in the opposite direction. Conversely, a negative slope represents a downward slant, implying that the object’s velocity is decreasing in a positive direction or accelerating in the opposite direction.

Imagine a car driving down the road. If the velocity-time graph shows a positive slope, we know the car is speeding up or moving at a constant speed. However, if the slope is negative, the car is slowing down or moving in reverse.

The slope of the velocity-time graph not only reveals the direction of motion but also serves as a mathematical tool. By calculating the slope, we can determine the average acceleration of the object over a given time interval. This acceleration quantifies how rapidly the object’s velocity is changing, further illuminating the dynamics of its motion.

Understanding positive and negative velocity is essential for interpreting velocity-time graphs and accurately describing an object’s movement. It’s a fundamental concept that underpins our comprehension of motion and guides us in predicting an object’s future trajectory.

Delving into Average Velocity: A Comprehensive Guide

Understanding Average Velocity

Average velocity, a pivotal concept in physics, describes the rate at which an object travels over a period of time. It’s the total displacement an object undergoes divided by the total time taken.

Interpreting a Velocity-Time Graph

A velocity-time graph is a graphical representation of an object’s velocity over time. The displacement is the vertical distance covered by the line on the graph, while the time is the horizontal distance. The slope of the line represents the object’s velocity.

Calculating Displacement from the Graph

To ascertain an object’s displacement from a velocity-time graph, subtract the initial position from the final position. This displacement indicates the net distance traveled by the object.

Calculating Average Velocity from the Graph

Average velocity is calculated by dividing the displacement by the total time. It measures the average rate of motion over the entire time interval.

Slope and Velocity

The slope of a line on a velocity-time graph is directly proportional to the object’s velocity. A positive slope indicates motion in the positive direction, while a negative slope indicates motion in the negative direction.

Positive and Negative Velocity

Positive velocity represents motion in the direction of increasing displacement, while negative velocity represents motion in the direction of decreasing displacement.

Example Calculation

Consider a velocity-time graph where an object moves from an initial position of 0 m at time 0 s to a final position of 100 m at time 10 s.

• Displacement = Final position – Initial position = 100 m – 0 m = 100 m
• Average velocity = Displacement ÷ Total time = 100 m ÷ 10 s = 10 m/s

Applications of Average Velocity

Average velocity finds practical applications in myriad fields:

• Determining the speed of a car based on its displacement and travel time
• Calculating the velocity of a projectile launched vertically upward and then downward
• Estimating the average speed of a runner over a race distance

Applications of Average Velocity: A Window into Object Motion

Understanding the concept of average velocity is essential for describing the motion of any object. It tells us how quickly and in which direction an object is moving over a given time interval. This knowledge has practical applications in various fields.

One common application of average velocity is determining the speed of a car. The speedometer in your car measures the average velocity over a short time interval. This number indicates how far you’ve traveled per unit time, typically expressed in miles per hour or kilometers per hour.

Another notable application lies in the field of projectile motion. Calculating the velocity of a projectile helps us predict its trajectory and determine where it will land. By knowing the initial velocity and acceleration due to gravity, we can estimate the projectile’s average velocity over its flight path.

Average velocity also plays a crucial role in sports. In running events, for instance, the average velocity of a runner determines their ranking and overall performance. By dividing the total displacement (the distance covered) by the total time, we can calculate an athlete’s average velocity.

In summary, average velocity is an important concept that helps us understand and interpret the motion of objects. Its applications extend from everyday scenarios like driving a car to complex calculations in fields like physics and engineering. By understanding this concept, we gain a deeper appreciation for the fascinating world of motion that surrounds us.