Unveil Function End Behavior: Horizontal, Vertical, And Slant Asymptotes

Describing the end behavior of functions involves identifying their long-term behavior as the independent variable approaches infinity or negative infinity. Horizontal asymptotes represent the function’s trend as it extends indefinitely in one direction, while vertical asymptotes indicate where the function approaches infinity or negative infinity. Slant asymptotes provide a more precise indication of the function’s behavior near a specific point. Understanding these concepts helps determine the overall shape and characteristics of a function, particularly for polynomials, where the degree and leading coefficient play a significant role. Additionally, the odd-even property of a function can influence its end behavior, showcasing symmetry or asymmetry.

End Behavior in Functions: Unveiling the Asymptotic Symphony

Understanding the end behavior of functions is crucial for grasping their overall shape and long-term tendencies. End behavior refers to how a function behaves as its input approaches infinity (either positive or negative) or as it approaches a specific finite value.

In the vast tapestry of mathematical functions, end behavior is a guiding light, illuminating the symphony of asymptotes that govern their trajectories. Asymptotes are imaginary lines that functions approach but never touch. They provide invaluable insights into a function’s ultimate destiny.

The three fundamental types of asymptotes are:

• Horizontal asymptotes, reflecting the function’s long-term trend.
• Vertical asymptotes, where the function becomes undefined and soars to infinity.
• Slant asymptotes, offering a glimpse into the function’s behavior as input approaches infinity along a slanted path.

By unraveling the mysteries of asymptotes, we unlock the secrets of a function’s end behavior. These imaginary lines serve as signposts, directing us toward the function’s ultimate destination.

End Behavior: Unraveling the Secrets of Functions

Embark on a journey into the realm of end behavior, the captivating phenomenon that governs the behavior of functions as they soar towards infinity. This guide will illuminate the different types of asymptotes, those guiding lights that shape the destiny of functions.

Asymptotes: Pathways to Understanding

Asymptotes are invisible boundaries that functions approach but never quite touch. They serve as gateways to understanding the end behavior of functions, providing insights into their ultimate trends and characteristics.

Horizontal Asymptotes: Guiding the Long-Term Trend

Horizontal asymptotes represent the ultimate destination of a function as it stretches towards infinity. These lines of tranquility indicate the long-term behavior of the function, foreshadowing its fate as it journeys into the unknown.

Vertical Asymptotes: Lines of Infinity

Vertical asymptotes mark the points where a function touches the sky. These lines of infinity separate the function’s domain, creating zones of existence and non-existence. Vertical asymptotes reveal the function’s limits, the boundaries beyond which it cannot venture.

Slant Asymptotes: A Glimpse of Infinity’s Embrace

Slant asymptotes offer a glimpse into the function’s destiny as it reaches infinity. These lines of compromise intersect the function at a single point, providing a steady guide to its ultimate fate. Slant asymptotes reveal the function’s asymptotic behavior, the pattern it follows as it approaches infinity’s alluring embrace.

Understanding End Behavior: A Comprehensive Guide

Types of Asymptotes: Gateways to End Behavior

Asymptotes are lines that a function approaches but never actually touches. They provide invaluable insights into the end behavior of a function, which describes how the function behaves as the input approaches infinity or negative infinity.

• Horizontal Asymptotes: These lines represent the function’s long-term trend. As the input goes to infinity or negative infinity, the function’s output approaches the horizontal asymptote, indicating that the function reaches a steady state.
• Vertical Asymptotes: These lines are infinite and indicate where the function’s output becomes undefined. As the input approaches the vertical asymptote, the function’s output grows infinitely large, either positively or negatively.
• Slant Asymptotes: These lines are oblique and represent the function’s long-term behavior. They show the direction in which the function’s output approaches infinity when the input goes to infinity or negative infinity.

How Asymptotes Influence the Behavior of Functions

Asymptotes play a crucial role in determining the end behavior of functions. They indicate:

• Long-Term Behavior: Horizontal asymptotes show the function’s ultimate value as the input approaches infinity or negative infinity.
• Discontinuities: Vertical asymptotes reveal points where the function is undefined, creating holes in the graph.
• Limits: Slant asymptotes provide information about the function’s output as the input goes to infinity or negative infinity, indicating limiting values.

Understanding the different types of asymptotes and their influence on end behavior is essential for analyzing and graphing functions effectively.

Horizontal Asymptotes: Guiding the Long-Term Trend

In the realm of functions, where graphs dance across the coordinate plane, asymptotes emerge as ethereal guides, shaping the paths of these mathematical entities. Among these asymptotic sentinels, horizontal asymptotes stand tall, dictating the function’s long-term trajectory.

Horizontal asymptotes, graceful lines parallel to the x-axis, serve as distant beacons, attracting the function’s graph as it embarks on its infinite journey. They represent the ultimate destiny of the function, the stable state it approaches as x ventures to infinity.

These horizontal lines of attraction hold a profound significance. They reveal the function’s long-term behavior, offering a glimpse into its distant future. Whether the graph ascends towards a positive value or descends towards a negative value, the horizontal asymptote provides crucial insight into the function’s asymptotic approach.

Furthermore, horizontal asymptotes serve as gateways to understanding other asymptotes. Their presence can signal the potential for vertical asymptotes or slant asymptotes, providing clues to the function’s overall behavior. They are essential elements in the tapestry of asymptotes, shedding light on the intricacies of the function’s graphical nature.

A Journey into the Realm of Asymptotes: Unveiling End Behavior

[Subheading] The Interconnected Symphony of Asymptotes

In the world of functions, asymptotes serve as gateways to understanding the ultimate destiny of the graph’s trend. These enigmatic lines guide us towards the function’s end behavior, revealing tantalizing clues about its behavior at the far ends of its domain.

Horizontal asymptotes, invisible horizons, paint a picture of the function’s long-term trend. They emerge when the graph approaches a specific horizontal path as it extends infinitely in either direction. These asymptotes unveil the function’s ultimate destination.

Vertical asymptotes, vertical barriers, signal infinite discontinuities in the graph. They divide the function’s domain into distinct regions, preventing the graph from crossing these forbidden lines. Vertical asymptotes offer pivotal insights into the function’s behavior near these points of discontinuity.

Finally, slant asymptotes, diagonal guides, provide a unique perspective on the function’s end behavior. They emerge when the graph approaches a diagonal line as it extends indefinitely. Slant asymptotes not only reveal the function’s ultimate direction but also offer clues about its long-term growth rate.

These three types of asymptotes intertwine harmoniously, each providing a distinct piece of the puzzle that is end behavior. Horizontal asymptotes indicate the long-term level, vertical asymptotes demarcate regions of discontinuity, and slant asymptotes reveal the ultimate direction and growth rate. Together, they form a symphony of lines that guide us through the function’s end behavior journey.

Vertical Asymptotes: Lines of Infinity

Picture this: You’re walking along a seemingly endless path, and suddenly, you encounter a towering, invisible wall. No matter how you try to push through, it remains impenetrable. This enigmatic wall represents a vertical asymptote in the realm of functions.

Vertical asymptotes are perpendicular lines that functions approach but never actually touch. Imagine a rocket ship hurtling towards the horizon. As it gets closer and closer, it appears to be heading straight for the meeting point, but it never quite reaches it. This is akin to how functions behave near vertical asymptotes.

The presence of a vertical asymptote indicates a discontinuity in the function. The function may have a hole at that point, where the graph abruptly jumps from one side to the other. Or, it may oscillate infinitely, never fully crossing the asymptote.

Identifying vertical asymptotes involves examining the denominator of a function. If the denominator contains a factor that equals zero at a particular value of the independent variable, then there is a vertical asymptote at that value.

For instance, consider the function f(x) = 1/(x-2). The denominator (x-2) equals zero when x = 2. Therefore, x = 2 is a vertical asymptote for this function. As x approaches 2 from either side, the function becomes infinite and approaches the asymptote.

Impact of Vertical Asymptotes on End Behavior and Asymptotes

Vertical asymptotes represent lines of infinity in the graph of a function. They occur when the denominator of a rational function approaches zero, causing the function to either increase or decrease rapidly without bound.

End Behavior:

Vertical asymptotes dictate the end behavior of a function. As the independent variable approaches the vertical asymptote from the left or right, the function’s value tends to either positive or negative infinity. This behavior is depicted by a graph that appears to approach the asymptote but never actually intersects it.

Influence on Asymptotes:

Vertical asymptotes can also influence the behavior of other asymptotes. For instance, if a function has both a vertical and a horizontal asymptote, the vertical asymptote can disconnect the function from the horizontal asymptote. This results in the function approaching the horizontal asymptote only from one side of the vertical asymptote.

Slant Asymptotes: A Glimpse of Infinity’s Embrace

In the world of functions, where graphs dance across the coordinate plane, there exist these fascinating creatures called slant asymptotes. Unlike their horizontal and vertical counterparts, slant asymptotes offer a unique perspective into the eternal dance of infinity.

Imagine a function stretching towards infinity, its graph seemingly spiraling into the celestial abyss. As you peer closer, you notice a faint line, a whisper of infinity’s embrace. This line is the slant asymptote, a guiding light that reveals the function’s ultimate destiny.

Slant asymptotes possess a fascinating equation: y = mx + b, where m represents the slope and b represents the y-intercept. This equation holds the key to understanding the end behavior of the function. As x tends to infinity, the function’s values approach the slant asymptote’s equation, gradually aligning with its path.

Moreover, slant asymptotes provide a glimpse into the function’s symmetry. If the function is an even function, the slant asymptote will be parallel to the x-axis. Conversely, if the function is an odd function, the slant asymptote will be parallel to either the x-axis or the y-axis.

In essence, slant asymptotes serve as celestial guides, illuminating the path of functions as they approach infinity’s enigmatic realm. Their presence whispers tales of long-term behavior, symmetry, and the infinite dance that unfolds in the vast expanse of mathematical space.

Slant Asymptotes: Revealing the True End Behavior

In the realm of functions, end behavior holds a special significance, providing insights into how these mathematical entities behave as their inputs approach infinity or negative infinity. Horizontal asymptotes and vertical asymptotes play crucial roles in determining this end behavior, but what about slant asymptotes? These elusive lines hold a unique power to unveil the true destiny of functions.

Imagine a function’s graph stretching endlessly toward the edges of the coordinate plane. As the input values become extremely large or small, the function’s output values may approach a non-horizontal line called a slant asymptote. This line represents the end behavior of the function, describing how the graph trends towards infinity.

How does a slant asymptote reveal this hidden behavior? By dividing the function’s numerator by its denominator and performing long division, we can obtain a quotient and a remainder. The quotient, when graphed, forms the slant asymptote. The remainder, when divided by the denominator, approaches zero as the input values approach infinity or negative infinity.

This subtle behavior has a profound impact on the end behavior of the function. The graph approaches the slant asymptote as the input values become extremely large or small, indicating a linear trend. This trend persists regardless of the distance from the asymptote, providing a glimpse into the function’s ultimate destination.

To summarize, slant asymptotes are not mere lines but gateways to understanding the end behavior of functions. By dividing the numerator by the denominator and observing the quotient and remainder, we unveil the function’s long-term trend. This knowledge empowers us to predict the behavior of functions even at the most extreme values of their inputs.

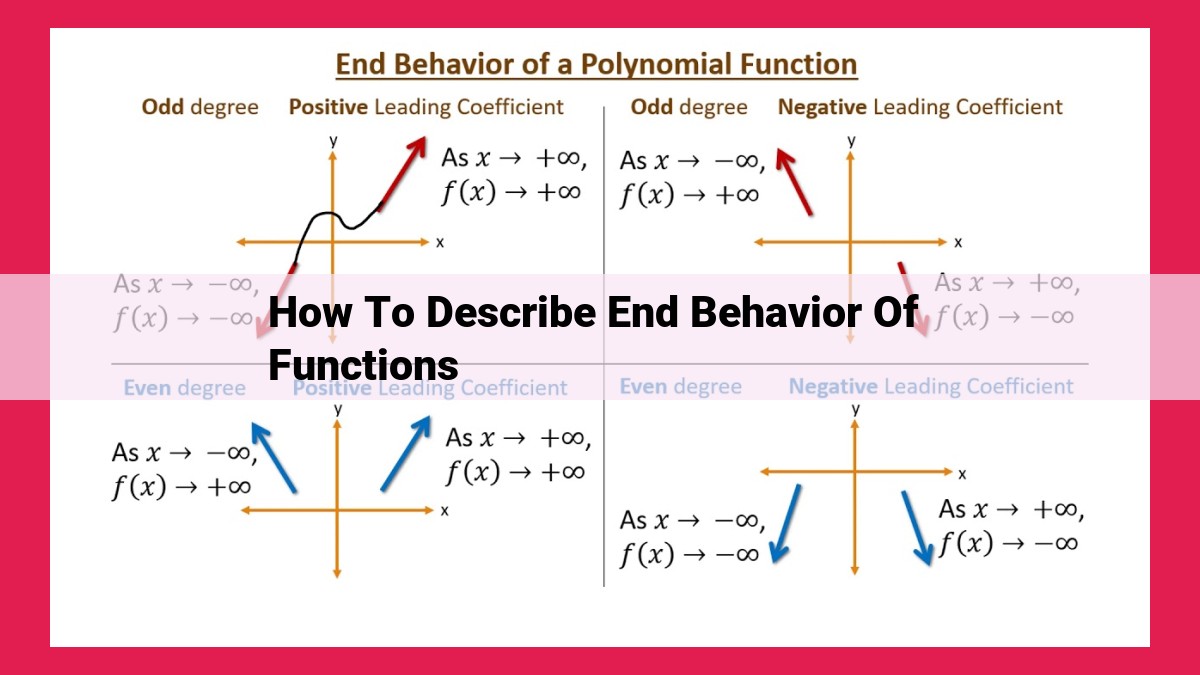
The role of degree and leading coefficient in determining end behavior.

Polynomial End Behavior: A Cocktail of Degree and Coefficient

As we delve into the fascinating world of polynomial functions, two crucial factors take center stage: degree and leading coefficient. These mathematical sorcerers determine the destiny of polynomials as they stretch towards infinity.

The degree of a polynomial, measured by the highest exponent of the variable, dictates its attitude at infinity. Odd-degree polynomials, like precocious teenagers, swing between positive and negative values as x grows without bounds. Even-degree polynomials, on the other hand, behave like seasoned adults, approaching a definitive limit as x ventures far away.

The leading coefficient, the commander-in-chief of the polynomial, holds the power to amplify or diminish the polynomial’s behavior. A positive leading coefficient propels the polynomial upwards towards infinity, while a negative coefficient sends it plummeting down.

Imagine a quadratic polynomial (degree 2). As x grows towards infinity, the polynomial’s behavior is governed by the square term (x²). If the leading coefficient is positive, the polynomial shoots up like a rocket, approaching positive infinity. If it’s negative, the polynomial dives like an eagle, plunging towards negative infinity.

Cubic polynomials (degree 3) follow a similar pattern. However, the odd degree introduces a twist: they switch between positive and negative values as x becomes large. A positive leading coefficient grants them a final resting place at positive infinity, while a negative leading coefficient banishes them to negative infinity.

This dance of degree and coefficient extends to higher-degree polynomials. The degree determines the polynomial’s long-term behavior, dictating whether it approaches infinity or a finite limit. The leading coefficient then tunes the polynomial’s attitude, controlling the direction and steepness of its ascent or descent towards the infinite abyss.

Polynomial End Behavior: A Tale of Degree and Leading Coefficient

Imagine a polynomial, a mathematical expression that consists of terms of the form ax^n, where a is a numerical coefficient and x is the variable. The degree of the polynomial is the highest exponent of x, and the leading coefficient is the coefficient of the term with the highest exponent.

These two factors play a crucial role in shaping the end behavior of the polynomial, that is, how the graph of the polynomial behaves as x approaches positive or negative infinity.

For even-degree polynomials, the leading coefficient determines the overall shape of the graph. If the leading coefficient is positive, the graph rises to the right (as x approaches infinity) and falls to the left (as x approaches negative infinity). If the leading coefficient is negative, the graph falls to the right and rises to the left.

Odd-degree polynomials exhibit a different behavior. The leading coefficient also determines the direction of the graph’s rise or fall, but the graph will always change direction as x approaches infinity or negative infinity. This is because odd-degree polynomials have a linear term, which dominates the behavior of the graph for large values of x.

The degree of the polynomial, on the other hand, affects the steepness of the graph. Higher-degree polynomials rise or fall more rapidly than lower-degree polynomials. This is because the higher the exponent, the greater the influence of the leading coefficient on the term’s contribution to the overall shape.

In summary, when analyzing the end behavior of polynomials, remember that the degree influences the steepness of the graph, while the leading coefficient determines the overall shape, with even- and odd-degree polynomials exhibiting distinct patterns. Understanding these relationships empowers you to make educated guesses about the behavior of polynomial graphs even without plotting them explicitly.

Definition and characteristics of odd and even functions.

Understanding End Behavior: A Comprehensive Guide

In the realm of functions, end behavior unveils the fascinating trajectories of graphs at the horizons of infinity. By understanding the types of asymptotes that guide these paths, we can decipher the long-term trends and unravel the mysteries that lie at the boundaries of mathematical landscapes.

Types of Asymptotes

Asymptotes, like celestial beacons, illuminate the end behavior of functions. They delineate the paths functions take as they approach infinity, revealing patterns and insights that shape their overall character.

• Horizontal Asymptotes: These graceful lines mark the level at which functions stabilize as they stretch towards the distant ends of the coordinate plane. They provide a glimpse of the long-term destiny of the graph, indicating its ultimate fate.

• Vertical Asymptotes: Like towering cliffs, vertical asymptotes represent points where functions approach infinity, becoming infinitely steep and unreachable. They partition the plane into forbidden zones, where the functions’ trajectories diverge to extremes.

• Slant Asymptotes: These oblique guides offer a unique perspective on end behavior. They depict the direction in which functions head asymptotically, providing a linear approximation of their behavior as they approach infinity.

Polynomial End Behavior

Polynomials, the building blocks of algebraic expressions, exhibit predictable end behavior dictated by their degree and leading coefficient. The degree, the highest exponent, determines the function’s steepness at infinity, while the leading coefficient reveals its direction of ascent or descent.

Odd and Even Functions

Odd and even functions, defined by their symmetry, display distinctive end behaviors. Odd functions, like mischievous jesters, exhibit zero symmetry, flipping their image around the origin. Even functions, on the other hand, possess a mirror-like quality, maintaining symmetry about the y-axis. These properties influence their end behavior, leading to distinct trajectories as they journey towards infinity.

Odd and Even Functions: A Symmetry Tale that Shapes End Behavior

As we delve into the fascinating world of functions, we encounter intriguing traits that shape their behavior at the ends of their domains. Among these traits, the odd-even property stands out as a key determinant of how functions approach infinity or negative infinity. Let’s embark on a storytelling journey to explore how the odd-even property casts its spell on end behavior.

The Tale of Odd Functions

Imagine a function that, when reflected across the y-axis, remains unchanged. This enigmatic entity is known as an odd function. It possesses a peculiar characteristic that manifests itself in its end behavior. As the input approaches positive or negative infinity, odd functions exhibit a symmetrical oscillation around the horizontal axis. This mesmerizing dance creates a pattern where the function approaches infinity and negative infinity alternately, never fully settling on either side.

The Symphony of Even Functions

In contrast to their odd counterparts, even functions behave with a different rhythm when mirrored across the y-axis. These harmonious entities remain identical to their original form upon reflection. Their end behavior is a captivating display of symmetry around the y-axis. As the input journeys to infinity or negative infinity, even functions approach infinity or negative infinity, gracefully aligning with the horizontal axis. This harmonious convergence paints a picture of unwavering stability.

The Interplay of Symmetry and End Behavior

The interplay between the odd-even property and end behavior is a tantalizing dance of mathematical elegance. Odd functions, with their alternating approach to infinity, evoke a sense of vibrant pulsation. Even functions, on the other hand, exude a serene steadiness as they align themselves with the horizontal axis. This interplay serves as a testament to the profound influence of symmetry in shaping the behavior of functions at the boundaries of their domains.

The odd-even property is a mesmerizing force that weaves its magic into the tapestry of function behavior. Its influence on end behavior is profound, painting a vibrant canvas of oscillation for odd functions and a serene symphony of alignment for even functions. As we navigate the complexities of the mathematical realm, let us always remember the enchanting tale of odd and even functions, a testament to the intricate beauty and symmetry that lies within.