Essential Guide To Area: Formulas, Properties, And Spatial Reasoning

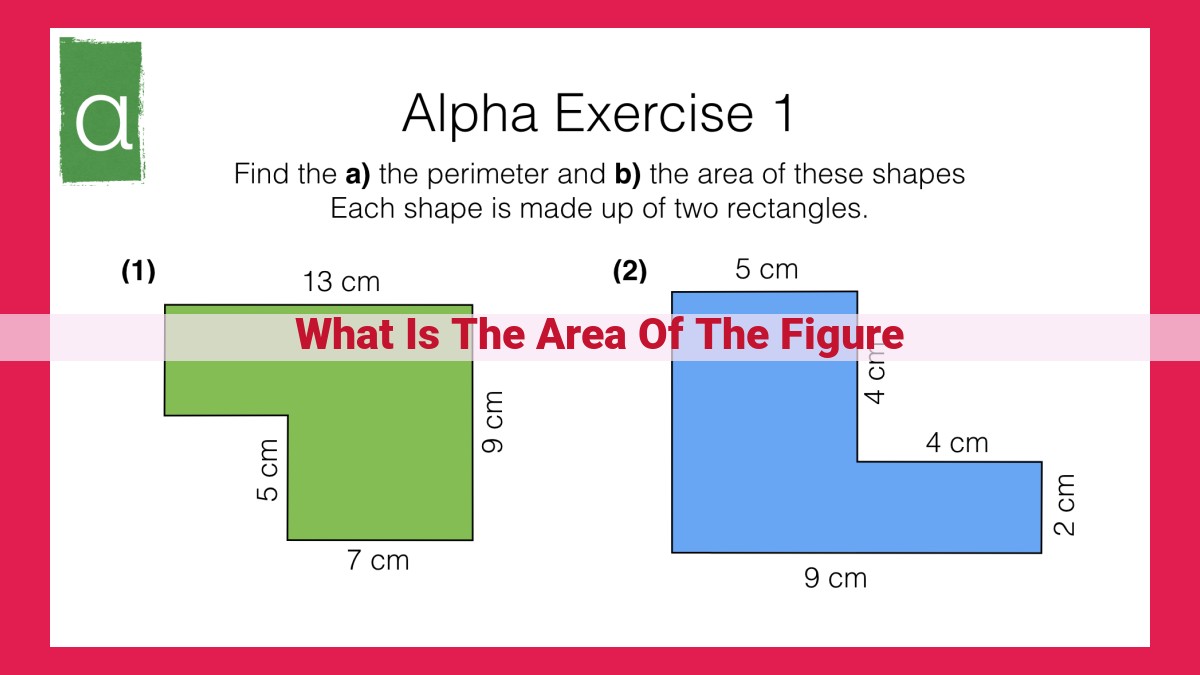
The area of a figure represents the amount of space contained within its boundaries. It measures the enclosed surface area and is expressed in square units. The area of different shapes can be calculated using specific formulas involving measurements such as length, width, height, and radius. Understanding the formulas for various shapes and their properties is essential for solving problems related to areas and spatial reasoning.

Understanding Perimeter: The Encompassing Boundary

In the realm of geometry, perimeter reigns supreme, defining the outermost boundary of any shape, be it a vibrant square or a whimsical circle. It’s the total length that encloses the shape, safeguarding its form and integrity.

Perimeter plays a pivotal role in understanding the size and shape of objects. It dictates the amount of fencing needed to enclose a garden, the length of thread required to stitch a hem, or the distance a runner must traverse around a track.

Enter the world of related concepts where perimeter intertwines with length, width, height, and even circumference. Length and width measure the sides of rectangles and squares, while height extends vertically from a shape’s base. Circumference, on the other hand, measures the outer boundary of a circle, a special shape with no corners.

By understanding perimeter, we unlock the key to deciphering the dimensions and boundaries of our surroundings, unraveling the secrets of geometry that shape our world.

Unraveling the Enigmatic Radius: A Journey to the Heart of Circles

In the realm of geometry, the radius emerges as a fundamental concept, defining the distance that connects the center of a circle to its edge. This enigmatic line holds the key to unlocking the mysteries of circular shapes, revealing their circumference, area, and diameter.

Like a navigator’s compass, the radius points the way, guiding us through the labyrinth of circular geometry. Its length determines the circle’s size, establishing the boundary between the shape’s interior and the outside world.

The radius is inextricably linked to its counterpart, the diameter. Together, they form the backbone of the circle, with the diameter being twice the length of the radius. This relationship provides a powerful tool for solving geometric puzzles, allowing us to calculate unknown measurements with ease.

But the radius’s influence extends beyond the circle’s physical dimensions. It plays a pivotal role in determining the circumference and area of this enigmatic shape. The circumference, the path’s length around the circle’s edge, is directly proportional to the radius. Doubling the radius doubles the circumference, creating a harmonious relationship between the two.

Similarly, the area, the interior space enclosed by the circle, is also dependent on the radius. Increasing the radius expands the area quadratically, leading to a geometric progression as the shape grows.

Understanding the radius is paramount for mastering the intricacies of circular geometry. It’s the linchpin that connects various concepts, enabling us to decipher the secrets of these timeless shapes. So, let us embrace the radius, delving into its mysteries and unlocking the geometric wonders that await us within.

Exploring Height:

• Define height as the vertical distance from the base to the top of a shape.
• Discuss related concepts: base, area, volume.

Exploring the Height of Geometric Shapes: A Guide to Understanding a Key Dimension

Within the realm of geometry, understanding the concept of height is crucial for unraveling the mysteries of various shapes. Height, in its simplest form, refers to the vertical distance measured from the base of a shape to its apex or highest point. This seemingly straightforward concept plays a pivotal role in determining the properties and characteristics of geometric figures.

Related Geometric Concepts

To fully grasp the significance of height, it’s essential to explore its relationship with other geometric concepts:

• Base: The base represents the bottom or foundation of a shape, providing a reference point for measuring height.
• Area: Height is directly linked to the area of a shape, which measures the amount of space it encloses.
• Volume: In three-dimensional shapes, height contributes to the volume, which quantifies the amount of space occupied by the shape.

Examples in Various Shapes

The concept of height manifests in different ways across geometric shapes:

• In a triangle, height is the perpendicular distance from the vertex (top point) to the opposite side (base).
• In a rectangle, height refers to the vertical distance between the top and bottom sides.
• In a cylinder, height measures the distance between the top and bottom circular faces.
• In a sphere, height is essentially synonymous with the radius, as it represents the distance from any point on the surface to the center.

Applications in Real-World Scenarios

Understanding height has practical applications in various fields:

• Architects and engineers use height when designing buildings and structures to ensure stability and functionality.
• Designers rely on height when creating objects that need to fit into specific spaces or meet ergonomic requirements.
• Landscapers use height to determine the appropriate angle of elevation for drainage systems.

Unraveling the Diameter: A Key Geometric Concept

In the intriguing realm of geometry, understanding the diameter is crucial. It represents the distance across the center of a circle, connecting two points on the circle’s circumference. This fundamental concept is intertwined with other geometric measurements, such as radius and circumference, forming the backbone of many shape-related calculations.

Defining the Diameter

Imagine a circle, a captivating shape with no corners or edges. Its diameter is the straight line that passes through the center, dividing the circle into two equal halves. This line segment, connecting two points on the circle’s rim, provides a snapshot of the circle’s overall size.

Diameter vs. Radius

The diameter and radius are closely related concepts. While the diameter bisects the circle, the radius connects the center to any point on the circumference. In fact, the diameter is twice the length of the radius. This simple relationship makes it easy to determine one measurement once the other is known.

Practical Applications

The diameter has various practical applications in everyday life. For instance, in engineering, measuring the diameter of a pipe is essential for determining its flow capacity. In carpentry, knowing the diameter of a cylindrical rod is crucial for selecting the right drill bit size. Moreover, the diameter of a planet or star provides insights into its physical dimensions.

Understanding the diameter of a circle is a fundamental geometric concept that unlocks a world of shape-related calculations. By grasping this concept, we can unravel the mysteries of circles and accurately measure their dimensions, paving the way for a deeper understanding of the world around us.

Delving into Side Length: Unraveling the Essence of Polygons

The world of geometry is a fascinating one, filled with intricate shapes and precise measurements. Among these geometric concepts, the side length holds a pivotal role in describing and understanding polygons.

A polygon, as the name suggests, is a plane figure bounded by straight line segments called sides. The side length of a polygon is simply the length of one of its sides. This fundamental measurement forms the cornerstone for defining the perimeter and area of a polygon.

Perimeter: A Walk Around the Polygon

The perimeter of a polygon is the total distance around its boundary. To calculate the perimeter, we simply add up the lengths of all its sides. For a regular polygon, where all sides are equal, the perimeter is simply the side length multiplied by the number of sides.

Area: Exploring the Interior

The area of a polygon represents the measure of its enclosed space. While the side length does not directly determine the area, it plays a crucial role in its calculation. For certain regular polygons, such as squares and equilateral triangles, the area can be expressed as a function of the side length alone.

Side Length and Related Concepts

In the realm of polygons, the side length is intertwined with other geometric concepts. For instance, the perimeter of a polygon is directly proportional to its side length. The greater the side length, the greater the perimeter.

Furthermore, the side length also influences the area of a polygon. While the relationship is more complex, the area generally tends to increase with increasing side length.

The side length of a polygon is a fundamental geometric concept that plays a vital role in defining its perimeter and area. By understanding the relationship between side length and these other measurements, we gain a deeper insight into the structure and properties of polygons.

Unraveling the Base: A Cornerstone of Shapes

In the world of geometry, understanding the concept of base is crucial for unraveling the mysteries of shapes. The base is the foundation upon which many geometric calculations are built. It serves as the starting point for measuring heights, calculating areas, and determining volumes.

Defining the Base

The base of a shape refers to its bottom side. It provides a stable platform for the shape to stand upon, like the foundation of a house. For example, in a triangle, the base is the horizontal line that forms the bottom of the shape. In a rectangle, the base is the longer side that runs parallel to the height.

Interrelation with Height and Area

The base plays a pivotal role in determining the shape’s height and area. Height, the vertical distance measured from the base to the top of the shape, is directly proportional to the base. As the base increases, so too does the height, allowing the shape to become taller or wider.

Similarly, the base has a significant impact on the shape’s area. Area is the measure of the surface enclosed within the shape’s boundaries. For example, in a rectangle, the area is calculated by multiplying the base by the height (A = base x height). As the base increases, the area of the rectangle increases, as there is more space enclosed within the shape.

Importance in Volume Calculations

The base also extends its influence to the calculation of volumes for three-dimensional shapes. Volume measures the amount of space occupied by a shape. For example, in a rectangular prism, the volume is determined by multiplying the base area by the height. As the base area increases, so too does the volume, signifying a larger space enclosed within the shape.

Examples in Real-World Applications

The concept of base finds practical applications in various fields:

• Architecture: Architects use the base dimension when designing buildings to ensure structural stability and space optimization.
• Engineering: Engineers calculate the load-bearing capacity of bridges and other structures based on the base area of their supporting elements.
• Manufacturing: Manufacturers rely on base dimensions to determine the size and shape of products, such as packaging materials and electronic devices.

Circumference of a Circle:

• Introduce the formula: C = 2πr
• Discuss the relationship between radius, diameter, and circumference.

Demystifying the Circumference of a Circle: A Tale of Geometry and Harmony

In the realm of geometry, the circle stands as an enigmatic figure, its simple yet profound beauty captivating mathematicians and artists alike. At the heart of this allure lies a fundamental concept: the circumference. Measuring the perimeter of this perfect shape unveils a mesmerizing relationship between its defining attributes.

The circumference of a circle is the total distance around its boundary. It is denoted by the letter “C” and expressed in the enchanting formula:

C = 2πr

Here, the Greek letter “π” (pi) is a constant that holds the mystical value of approximately 3.14. It represents the ratio of a circle’s circumference to its diameter, a fundamental relationship that has fascinated mathematicians throughout history.

• The Radius: A Guiding Light to the Circle’s Edge:

The radius of a circle is the distance from its center to any point on its perimeter. Symbolized by the letter “r,” the radius serves as a guiding light, illuminating the connection between the circle’s shape and its circumference. In the formula C = 2πr, the radius plays a pivotal role, revealing the proportional relationship between these two measurements.

• The Diameter: A Bridge Between Center and Circumference:

The diameter of a circle is the distance across its center. Denoted by the letter “d,” the diameter forms a bridge between the circle’s core and its boundary. When we double the radius, we obtain the diameter, creating an elegant symmetry that further deepens our understanding of the circle’s geometry.

• The Symphony of Circumference, Radius, and Diameter:

The circumference, radius, and diameter engage in a harmonious dance, each playing a distinct yet intertwined role in defining the circle’s essence. The circumference represents the distance traveled along the boundary, capturing the circle’s outer reach. The radius, like a guiding hand, directs our path to the circle’s center. And the diameter, spanning its width, connects these elements, completing the circle’s geometric symphony.

Area of a Square: Unveiling the Relationship between Side Length and Area

In the realm of geometry, where shapes dance and formulas reign supreme, there’s a fundamental concept that governs the area occupied by these geometric entities: the area of a square.

Imagine a square, a shape with four equal sides. The area of a square isn’t just a number; it’s a story of how the side length of the square dictates the amount of space it encompasses.

At the heart of this story lies a magical formula: A = s^2. Here, A represents the area of the square, and s is the length of its side. It’s a simple yet powerful equation that unlocks the secrets of a square’s area.

Think of it this way: as the side length of a square increases, so does its area. It’s like a symphony where the side length is the conductor, orchestrating the expansion of the square’s area.

For instance, if you have a square with a side length of 2 units, its area will be 4 square units (A = 2^2 = 4). But if you double the side length to 4 units, the area quadruples to 16 square units (A = 4^2 = 16).

This relationship is the cornerstone of understanding the area of a square. It’s a tale of proportions, where the area grows proportionally to the square of the side length.

So, the next time you encounter a square, remember this geometric dance between side length and area. It’s a story worth cherishing, for it reveals the hidden harmonies that shape our world.

Understanding the Area of a Rectangle

In the realm of geometry, shapes hold a fascinating allure, each with its unique characteristics. Among these geometric wonders, the rectangle stands out as a versatile and widely encountered shape. It boasts two pairs of parallel sides and four right angles, making it an object of both aesthetic and mathematical intrigue.

In this article, we embark on a journey to unravel the mysteries surrounding the area of a rectangle, a fundamental concept that unlocks the secrets of measuring the space enclosed within this captivating shape.

The Formula: A Tale of Length and Width

The area of a rectangle, denoted by the symbol A, is calculated using a straightforward formula: A = l x w. This formula serves as a mathematical cornerstone, representing the product of the rectangle’s length (l) and its width (w).

Unveiling the Relationship

To grasp the essence of this formula, it is imperative to comprehend the relationship between the rectangle’s length and width. The length refers to the horizontal measurement of the rectangle, while the width signifies its vertical measurement.

By multiplying the length and width, we essentially determine the number of square units that can be accommodated within the rectangle’s boundaries. For instance, a rectangle with a length of 5 units and a width of 3 units will have an area of 15 square units.

Practical Applications in Our World

The concept of area finds countless applications in our daily lives. Architects and engineers rely on it to calculate the floor space of buildings and the coverage of roofs. Landscapers use it to determine the amount of lawn or garden to maintain. Artists and designers employ it to plan the dimensions of paintings, sculptures, and other creative endeavors.

In conclusion, understanding the area of a rectangle is not merely an academic exercise but a valuable tool with practical significance in various fields. By delving into the formula and its implications, we gain a deeper appreciation for the geometry that shapes our world.

Area of a Triangle:

• Introduce the formula: A = (1/2) x b x h
• Explain the relationship between base, height, and area.

The Intriguing Concept of Triangle Area: Unlocking the Secrets of Geometric Precision

Geometry, the fascinating world of shapes and their properties, offers a treasure trove of concepts that intrigue and empower us. Among these, understanding the area of a triangle is a fundamental skill that unlocks a deeper appreciation for this enchanting shape.

The area of a triangle represents the space enclosed within its boundaries. It is a measure of its two-dimensional extent and is calculated using a specific formula: A = (1/2) x b x h.

In this formula, b denotes the base of the triangle, which is any side chosen as the reference. h represents its height, which is the perpendicular distance from the base to the opposite vertex.

To visualize this concept, imagine a rectangular garden. The length of the garden represents the base (b), while its width serves as the height (h). The area of this garden is calculated by multiplying the length (base) by the width (height).

Similarly, in the case of a triangle, the base (b) represents one of its sides, and the height (h) is the distance from this base to the vertex not on that side. Multiplying the base by half the height gives us the area of the triangle.

The formula A = (1/2) x b x h allows us to calculate the area of any triangle, regardless of its shape or size. This understanding empowers us to solve practical problems, such as determining the coverage area of a tarp or the amount of paint required to cover a triangular wall.

By unraveling the concept of triangle area, we gain a deeper appreciation for the intricacies of geometry and its applications in our everyday lives. It is a testament to the power of mathematics and the beauty that unfolds when we explore its captivating world.

Understanding the Trapezoid: Delving into Its Area

In the realm of geometry, where shapes come to life, there exists a unique quadrilateral called the trapezoid. Unlike its rectangular cousin, the trapezoid boasts two parallel sides, making it both distinctive and intriguing. Among its many characteristics, understanding its area is paramount in unlocking its geometric secrets.

Unveiling the Trapezoid’s Area: A Mathematical Formula

At the heart of the trapezoid’s area lies a formula that encapsulates the relationship between its dimensions: A = (1/2) x h x (b1 + b2)

Where:

• A represents the area of the trapezoid
• h signifies the height, the perpendicular distance between the parallel sides
• b1 and b2 denote the lengths of the parallel sides

This formula provides a roadmap for calculating the trapezoid’s area. By plugging in the appropriate values of its height and parallel side lengths, we can unlock the mystery of its surface area.

Exploring the Formula: A Deeper Dive

The trapezoid’s area formula embodies a meaningful interplay between its dimensions. The height, like a vertical bridge, connects the two parallel sides, establishing the distance between them. The (b1 + b2) term, representing the sum of the parallel side lengths, captures the trapezoid’s width.

Multiplying the height by this sum, we effectively calculate the area of the trapezoid’s base. However, the trapezoid’s uniqueness lies in its non-parallel sides, which create an asymmetry that requires division by 2. This adjustment ensures an accurate representation of the trapezoid’s true area.

Harnessing the Formula: Applications in the Real World

The trapezoid’s area formula finds practical applications in various fields. Architects utilize it to calculate the surface area of roofs with slanted sides. Engineers leverage it to determine the area of trapezoidal-shaped structures, ensuring their stability and load-bearing capacity. Even in everyday life, we encounter trapezoids in the form of tabletops, sails, and even slices of pizza. Understanding its area empowers us to make precise calculations and design effective solutions in these and countless other contexts.

Geometric Concepts: Understanding Shapes and Their Measurements

Embark on an enlightening journey into the fascinating world of geometric concepts, where we’ll explore the key dimensions and properties that define the shapes around us. From understanding perimeter to unraveling the secrets of area, we’ll delve into the essentials of geometry in a captivating storytelling style.

Perimeter: The Boundary’s Journey

Imagine a shape as a path to be traversed. The perimeter is the total distance you’d need to walk along its boundary, encompassing length, width, height, and even circumference for circles. It measures the shape’s outer edge, giving us a sense of its size.

Radius: The Circle’s Heart

Picture a circle as a celestial body, with the radius being the celestial line connecting its center to its edge. It defines the circle’s size and is closely related to diameter, circumference, and area, providing insights into the circle’s dimensions.

Height: Stretching from Base to Summit

Height is the vertical dimension, the distance from a shape’s base to its highest point. For mountains and skyscrapers alike, height gives us a sense of their towering presence and helps us understand their proportions.

Diameter: The Circle’s Span

Diameter is the circle’s longest chord, stretching from one edge to the opposite edge through the center. It’s twice the radius and closely linked to circumference, providing another perspective on the circle’s size.

Side Length: Defining the Polygon’s Boundary

Polygons are shapes defined by straight sides, each with a specific length. Side length determines the shape’s perimeter and area, playing a crucial role in understanding its dimensions and properties.

Base: The Foundation of Shapes

The base is the bottom side of a shape, upon which its other dimensions are built. It’s a fundamental element for calculating area and volume, providing a stable foundation for understanding a shape’s structure.

Circumference of a Circle: A Curved Journey

The circumference of a circle is the distance around its outer edge, a continuous path that encapsulates its curved nature. It’s calculated using the formula C = 2πr, where ‘r’ represents the radius, giving us a measure of the circle’s length.

Area of a Square: A Uniform Canvas

The area of a square is the amount of surface it covers, a uniform region bounded by four equal sides. It’s calculated using the formula A = s², where ‘s’ represents the length of each side, providing a measure of the square’s surface size.

Area of a Rectangle: A Lengthy and Wide Canvas

The area of a rectangle is the amount of surface it covers, a rectangular region defined by length and width. It’s calculated using the formula A = l x w, where ‘l’ represents the length and ‘w’ represents the width, giving us a measure of the rectangle’s surface size.

Area of a Triangle: A Triangular Patch

The area of a triangle is the amount of surface it covers, a triangular region bounded by three sides. It’s calculated using the formula A = (1/2) x b x h, where ‘b’ represents the base and ‘h’ represents the height, providing a measure of the triangle’s surface size.