Analyzing Mean Differences: Calculating, Interpreting, And Testing Significance

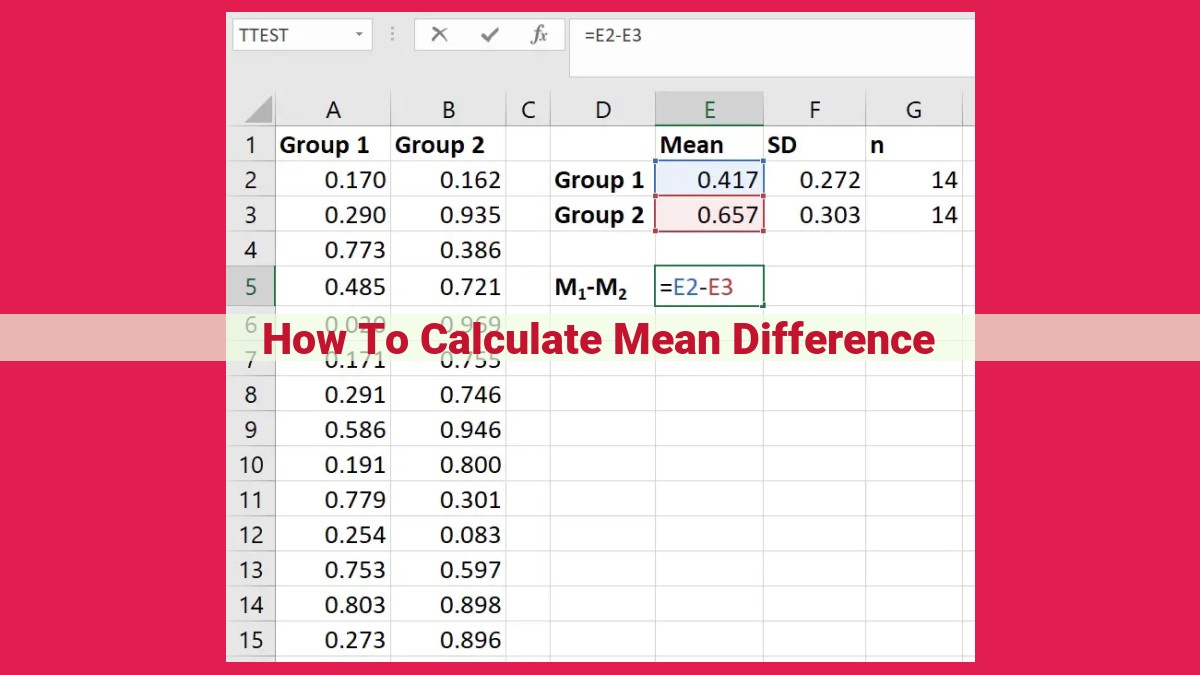
To calculate the mean difference between two datasets, subtract the mean of the first dataset from the mean of the second dataset. The raw difference represents the numerical difference between the means. The absolute difference ignores the direction of the difference and provides the magnitude. The percentage difference expresses the difference as a proportion of the smaller mean. The mean difference provides an estimate of the average difference between the observations. The confidence interval provides a range within which the true mean difference is likely to fall. Hypothesis testing, using t-tests or ANOVA, determines if the mean difference is statistically significant. Effect size measures, like Cohen’s d, quantify the magnitude of the difference relative to the variability within the datasets. Power analysis helps determine the sample size needed to detect a significant difference.

The Power of Comparison: The Importance of Mean Difference Calculation

In the realm of data analysis, comparison reigns supreme. It’s the key to unlocking insights, making informed decisions, and driving meaningful outcomes. At the heart of data comparison lies a crucial concept: mean difference calculation.

Imagine you’re a researcher conducting an experiment to evaluate the effectiveness of two different teaching methods. You collect data on student performance and want to determine if there is a significant difference between the two methods. That’s where mean difference calculation comes into play.

It’s a statistical tool that quantifies the average difference between two data sets. This difference can be calculated in various ways, each providing valuable information. By understanding the concepts behind mean difference calculation, you can empower your data analysis and make comparisons that lead to actionable insights.

Concepts for Calculating Mean Difference

In the world of data analysis, comparing different datasets is crucial. One of the most common ways to do this is by calculating the mean difference. The mean difference, also known as the average difference, quantifies the central tendency of the differences between two sets of data.

Raw Difference, Absolute Difference, and Percentage Difference

The simplest form of mean difference is the raw difference. This is simply the difference between the two data points without any transformation. The absolute difference is similar to the raw difference, except that it takes the absolute value, eliminating any negative signs. The percentage difference expresses the difference as a percentage of one of the data points, providing a relative comparison.

Mean Difference, Standard Deviation, and Standard Error

The mean difference is calculated by taking the average of the raw differences over all data points. The standard deviation of the differences measures the spread or variability of the differences. It indicates how much the differences vary from the mean difference. The standard error of the mean difference is a measure of how much the sample mean difference is likely to vary from the true mean difference in the population.

Confidence Interval

The confidence interval provides a range of values within which the true mean difference is likely to lie. It is constructed based on the sample mean difference, the standard error of the mean difference, and a level of confidence (usually 95%). The confidence interval helps determine whether the mean difference is statistically significant.

Calculating the mean difference and related statistics is essential for comparing datasets and making informed conclusions. By understanding these concepts, researchers and analysts can effectively evaluate data, identify meaningful differences, and draw valid inferences from their findings.

Statistical Testing and Interpretation: Unveiling the Mean Difference’s Significance

In the realm of data analysis, comparing data sets is crucial for drawing meaningful conclusions. One of the key statistical tools employed for this purpose is the mean difference, which measures the average difference between two data sets. However, simply calculating the mean difference is not enough; we need to assess its statistical significance to determine if the observed difference is likely to be due to chance or a true underlying difference between the data sets.

This is where statistical testing comes into play. Hypothesis testing allows us to test whether the observed mean difference is statistically significant, meaning it’s unlikely to have occurred by chance. One common hypothesis test for mean difference is the t-test, which is used when comparing two normally distributed data sets. The t-test calculates a t-statistic, which is then compared to a critical value to determine if the difference is statistically significant.

Another statistical test for mean difference is ANOVA (Analysis of Variance). ANOVA is used when comparing more than two data sets or when comparing data sets with non-normal distributions. ANOVA calculates an F-statistic, which is then compared to a critical value to determine if there is a statistically significant difference between the means of the data sets.

The Power of P-Values

When conducting hypothesis testing, we use a p-value to determine the statistical significance of the mean difference. The p-value represents the probability of observing the actual mean difference or a more extreme difference, assuming there is no real difference between the data sets. A low p-value (typically less than 0.05) indicates a statistically significant difference, as it suggests that the observed difference is unlikely to have occurred by chance.

Unveiling the Effect Size

Beyond statistical significance, it’s important to quantify the effect size of the mean difference. This measure provides information about the magnitude of the difference and its practical importance. Cohen’s d and eta squared are two commonly used effect size measures. Effect size helps us determine how meaningful the mean difference is and whether it has substantial implications for our research or application.

Quantifying the Impact: Delving into Effect Size Measures

When comparing two data sets, a mere mean difference tells only part of the story. The effect size, a numerical value, provides a more comprehensive understanding of the magnitude and significance of the difference. Embark on a journey to decode the significance of effect size measures, the cornerstone of data comparison.

Introducing Cohen’s d and Eta Squared

Effect size measures, like Cohen’s d and eta squared, quantify the size of the difference between data sets relative to their sample variability. Cohen’s d, a widely used measure, indicates the standardized difference between means, taking into account the standard deviation of the data. Eta squared, on the other hand, measures the proportion of variance explained by the difference between means.

Measuring the Impact of Effect Size

The effect size value conveys the magnitude of the difference between data sets. A small effect size indicates a minor difference, while a large effect size suggests a substantial disparity. Interpreting the effect size requires context and knowledge of the specific field. In psychology, for example, a Cohen’s d of 0.2 is considered small, 0.5 moderate, and 0.8 large.

Significance of Effect Size

Statistical significance tests alone are insufficient to fully grasp the impact of a difference. Effect size reveals practical significance, indicating the extent to which the observed difference is meaningful in the real world. A statistically significant difference may have a negligible effect size, while a non-significant difference might still have practical implications.

Quantifying the effect size is crucial for comprehensive data analysis. By understanding the concepts of Cohen’s d and eta squared, you can gauge the magnitude and significance of differences between data sets. This knowledge empowers you to make informed judgments about the relevance and impact of your findings, ensuring that your interpretations are both scientifically sound and practically valuable.

Power Analysis and Sample Size Determination in Mean Difference Calculations

When conducting statistical comparisons between two or more data sets, it’s crucial to ensure that the findings are not solely due to chance. Power analysis plays a vital role in determining the necessary sample size required to detect a meaningful mean difference between the data sets.

Power analysis addresses the probability of correctly rejecting the null hypothesis (which assumes no difference between the data sets) when it is actually false. A high power (typically set at 0.8 or 0.9) indicates a strong chance of detecting a significant mean difference, while a low power suggests a higher likelihood of failing to identify a difference.

The sample size required for a particular power analysis is influenced by several factors, including:

• Effect size: The magnitude of the expected mean difference between the data sets.
• Significance level: The probability of rejecting the null hypothesis when it is actually true (typically set at 0.05).
• Variability within the data: Measured by the standard deviation of each data set.

Using statistical software or online calculators, researchers can perform power analyses to determine the minimum sample size necessary to achieve a desired power level for their specific research question. This process helps ensure that the findings are statistically significant and not simply due to random variation. If the actual sample size is smaller than the calculated sample size, the power of the analysis will be lower and the ability to detect a significant difference will be reduced.

Applications and Examples of Mean Difference Calculations

In the realm of data analysis, mean difference calculations play a pivotal role across a wide spectrum of fields. Let’s delve into some real-world examples to illustrate their significance:

Statistics:

• Comparing Treatment Groups: Researchers conducting clinical trials often use mean difference calculations to assess the effectiveness of different treatment regimens. By comparing the mean outcome scores of experimental and control groups, they can determine whether the treatment had a significant impact.

Psychology:

• Assessing Cognitive Abilities: Psychologists use mean difference calculations to compare the cognitive performance of different groups, such as individuals with and without a certain condition. This helps identify significant differences in areas such as memory, attention, and problem-solving abilities.

Business:

• Market Research: Companies conduct market surveys to gather data on consumer preferences. By calculating the mean difference between the ratings of different products or services, they can identify the most appealing offerings and target their marketing efforts accordingly.
• Sales Analysis: Sales teams use mean difference calculations to compare the average sales volume of different sales representatives or regions. This helps identify areas of improvement and optimize sales strategies.

Additional Examples:

• Education: Educators compare mean test scores of classes or students to assess academic progress and identify areas where additional support is needed.
• Health Sciences: Researchers use mean difference calculations to compare the effectiveness of different therapies or treatments in improving patient outcomes.
• Manufacturing: Quality control engineers use mean difference calculations to ensure that products meet specified standards and specifications.

By quantifying the differences between data sets, mean difference calculations provide valuable insights into the effectiveness of interventions, the characteristics of different populations, and the performance of various systems. They serve as a fundamental tool for making informed decisions and driving data-driven progress in diverse fields.