Acid-Base Titration: Determining Equivalence Point Ph For Optimal Accuracy

To determine pH at the equivalence point, identify the steepest section of the titration curve. Calculate pH using the Henderson-Hasselbalch equation, which relates pH to acid concentration and dissociation constant (pKa). For strong acid-strong base titrations, the equivalence point represents complete neutralization, allowing for direct calculation of pH based on the moles of reactants.

• Define pH and its relevance in acid-base reactions.
• State the purpose of the guide: to determine pH at the equivalence point.

pH and the Equivalence Point: A Comprehensive Guide

In the realm of acid-base chemistry, understanding pH is crucial, as it reveals the acidity or basicity of a solution. This guide aims to equip you with the knowledge to determine pH at the equivalence point, a critical concept that forms the foundation of many chemical applications.

What is pH and Why is it Important

pH, the measure of hydrogen ion concentration, is expressed on a logarithmic scale from 0 to 14. A neutral solution has a pH of 7, while acidic solutions have pH values below 7 and basic solutions have pH values above 7. pH plays a vital role in numerous chemical reactions and is key to understanding various chemical processes.

The Equivalence Point: A Chemical Landmark

The equivalence point in an acid-base titration represents the moment when the moles of acid are equal to the moles of base. It marks the complete reaction of the reactants and is a crucial point for determining pH.

Equivalence Point: The Turning Tide in Acid-Base Titrations

Imagine a tense battleground where two formidable armies clash over the control of a vital resource. This resource, the equivalence point, marks the point where an acid and a base have completely neutralized each other, leaving a legacy of equal and neutralized forces.

The equivalence point is the ‘sweet spot’ of an acid-base titration, where the moles of acid and base present are ‘locked in an equal embrace’. At this juncture, the reaction has consumed exactly enough of both reactants to form a neutral solution that will no longer react with either acid or base. It’s like a delicate handshake, where neither party overpowers the other.

So, what makes this equivalence point so significant? For one, it allows chemists to determine the exact concentration of an unknown acid or base using a process called titration. By adding a known volume of one reactant to a known volume of the other reactant, while carefully monitoring the pH, chemists can pinpoint the exact moment when the equivalence point is reached. It’s like finding the ‘golden ratio’ in a chemical reaction.

Determining the Equivalence Point in Acid-Base Titrations: A Comprehensive Guide

The Tale of the Titration Curve

In the realm of chemistry, where acids and bases dance in harmony, there’s a pivotal moment known as the equivalence point. This is the point at which the reactants, an acid and a base, have completely neutralized each other. To understand how to determine the equivalence point, we must delve into the intriguing world of titration curves.

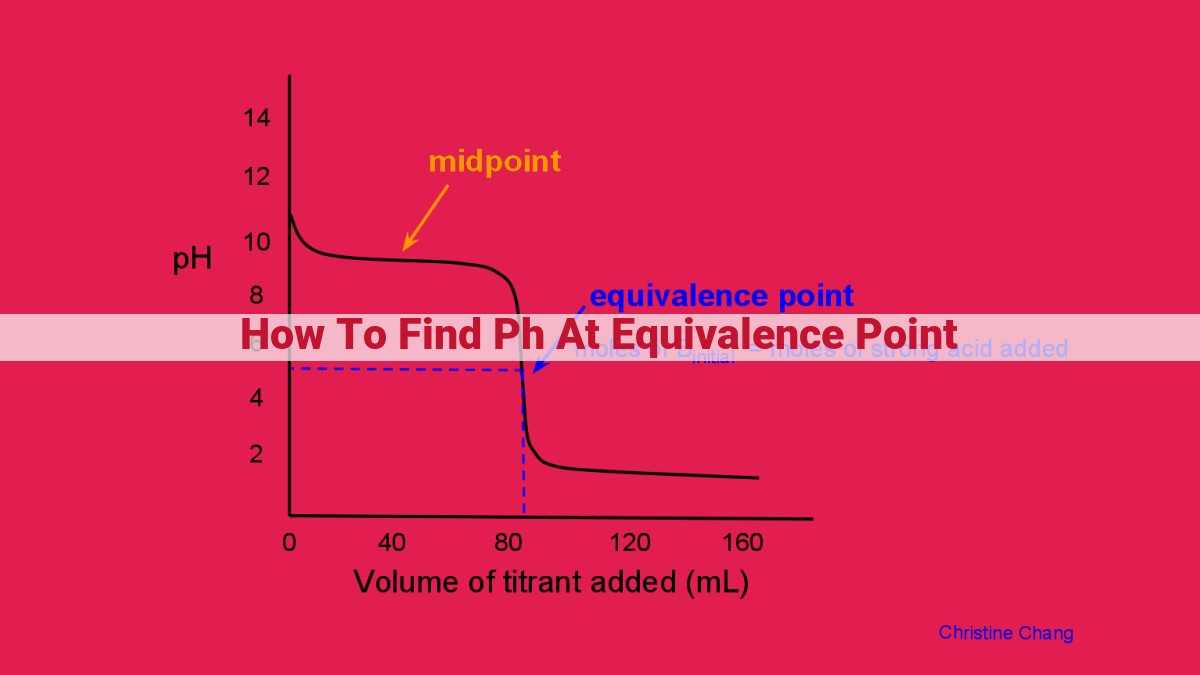
A titration curve is a graphical representation that depicts the pH of a solution as a function of the volume of base added. As the base is gradually added, the pH of the solution increases. The equivalence point is marked by the steepest section of the curve. This is because at this point, the buffering capacity of the solution is at its minimum, and a small addition of base causes a significant change in pH.

By examining the titration curve, we can visually identify the equivalence point. The point where the slope of the curve is greatest corresponds to the equivalence point. This method provides a quick and convenient way to approximate the equivalence point, particularly for weak acid-strong base titrations.

The Relationship Between pH and Ion Concentration

Understanding the concept of pH is crucial for determining the equivalence point. pH is a measure of the acidity or basicity of a solution. It is defined as the negative logarithm (base 10) of the hydrogen ion concentration ([H+]).

• Neutral solutions have a pH of 7, indicating an equal concentration of hydrogen ions and hydroxide ions ([OH-]).
• Acidic solutions have a pH less than 7, indicating a higher concentration of hydrogen ions.
• Basic solutions have a pH greater than 7, indicating a lower concentration of hydrogen ions.

The Henderson-Hasselbalch Equation and pKa

For weak acids, the Henderson-Hasselbalch equation provides a mathematical tool to calculate pH. This equation relates pH to the acid’s dissociation constant (Ka) and the relative concentrations of the weak acid (HA) and its conjugate base (A-).

pH = pKa + log([A-]/[HA])

The pKa value is a measure of the strength of a weak acid. Lower pKa values indicate stronger acids. By knowing the pKa of the weak acid and measuring the relative concentrations of [A-] and [HA], we can calculate the pH of the solution.

Calculating pH at the Equivalence Point

In the case of weak acid-strong base titrations, the equivalence point corresponds to the complete neutralization of the weak acid. At this point, all of the weak acid has reacted with the strong base, forming a salt and water.

Using the Henderson-Hasselbalch equation, we can derive a formula to calculate the pH at the equivalence point:

pH = (1/2)pKa + (1/2)log([Salt])

This formula takes into account the concentration of the salt formed at the equivalence point. By measuring or calculating this concentration, we can accurately determine the pH at the equivalence point.

pH and Ion Concentration: Understanding the pH Spectrum

Have you ever wondered why some solutions taste sour while others are bitter? It all comes down to their pH level. pH is a measure of the acidity or alkalinity of a solution, and it’s determined by the concentration of hydrogen ions (H+) in that solution.

The pH scale ranges from 0 to 14. Neutral solutions have a pH of 7, acidic solutions have a pH below 7, and basic (or alkaline) solutions have a pH above 7. The lower the pH, the higher the concentration of hydrogen ions, and the more acidic the solution.

The pH of a solution has a profound impact on various chemical and biological processes. For instance, the pH of our blood is tightly regulated around 7.35, as even slight deviations can lead to serious health issues. Similarly, many enzymes, proteins, and other biological molecules function optimally within a specific pH range.

Understanding pH is critical in various fields, including chemistry, biology, medicine, and environmental science. By understanding the relationship between pH and ion concentration, we can better understand and manipulate the properties of solutions and optimize chemical reactions.

The Henderson-Hasselbalch Equation: Unraveling the Secrets of Weak Acid pH

In the realm of chemistry, understanding the pH of a solution is paramount for a multitude of applications. When it comes to weak acids, the Henderson-Hasselbalch equation serves as an invaluable tool for deciphering this crucial parameter.

The Henderson-Hasselbalch equation is a mathematical formula that allows us to calculate the pH of a weak acid solution. It is named after its creators, Lawrence Henderson and Karl Hasselbalch, who developed it in the early 20th century.

The equation is:

pH = pKa + log([A-]/[HA])

where:

• pH is the pH of the solution
• pKa is the dissociation constant of the weak acid
• [A-] is the concentration of the conjugate base of the weak acid
• [HA] is the concentration of the weak acid

The dissociation constant (pKa) is a measure of how strongly an acid dissociates in water. The lower the pKa, the stronger the acid. Conversely, the higher the pKa, the weaker the acid.

The conjugate base of a weak acid is the species that is formed when the acid dissociates. For example, when acetic acid (CH3COOH) dissociates, it forms the acetate ion (CH3COO-).

The Henderson-Hasselbalch equation can be used to calculate the pH of a weak acid solution at any point in the titration process. However, it is particularly useful for calculating the pH at the equivalence point. The equivalence point is the point in a titration where the moles of acid and base are equal. At this point, the solution is completely neutralized and the pH is equal to the pKa of the weak acid.

To calculate the pH at the equivalence point, simply plug the pKa of the weak acid into the Henderson-Hasselbalch equation and solve for pH.

pH = pKa

The Henderson-Hasselbalch equation is a powerful tool for understanding the pH of weak acid solutions. It is essential for a variety of chemical applications, including:

• Buffer solutions: Buffers are solutions that resist changes in pH when small amounts of acid or base are added. The Henderson-Hasselbalch equation can be used to design buffer solutions with a specific pH.
• Acid-base titrations: Acid-base titrations are used to determine the concentration of an unknown acid or base. The Henderson-Hasselbalch equation can be used to calculate the pH of the solution at any point in the titration process.
• Biological systems: The pH of biological fluids is critical for maintaining proper cell function. The Henderson-Hasselbalch equation can be used to understand the pH of blood, urine, and other bodily fluids.

pKa and Acid Strength

In the realm of weak acids, besides understanding their behavior, another crucial concept emerges: pKa. This enigmatic term shares an intimate relationship with the dissociation constant, a numerical value that reflects the acid’s strength. Allow us to shed light on this fascinating connection.

The dissociation constant (Ka) quantifies the extent to which a weak acid dissociates into its component ions in an aqueous solution. It represents the equilibrium constant for the dissociation reaction. The higher the Ka, the more readily the acid dissociates, indicating a stronger acid.

pKa is the negative logarithm of the dissociation constant, mathematically expressed as:

pKa = -log(Ka)

Therefore, a lower pKa corresponds to a higher Ka, implying a stronger acid. This inverse relationship helps us gauge the relative strengths of weak acids. Acids with lower pKa values are more prone to dissociate, releasing more hydrogen ions (H+) and lowering the solution’s pH.

Understanding pKa is essential for comprehending the behavior of weak acids in various chemical contexts. It allows us to predict the extent of dissociation, estimate pH values, and design experiments involving acid-base reactions.

Neutralization Reaction: The Dance of Acids and Bases

In the realm of chemistry, the interaction between acids and bases is akin to a graceful dance, where these opposing forces come together to create a harmonious equilibrium. A neutralization reaction is the epitome of this delicate balance, where an acid and a base unite to form a neutral solution.

Imagine acid molecules as stern gatekeepers, protectively holding onto hydrogen ions (H+). Base molecules, on the other hand, are the benevolent hosts, eagerly accepting H+ ions into their embrace. When an acid and a base encounter each other, a captivating exchange takes place. The acid surrenders its H+ ions to the base, leading to the formation of salt and water.

Salt, the product of this chemical union, is a compound composed of the cation from the base and the anion from the acid. Water, the universal solvent, serves as the neutral byproduct that balances the equation. In a strong acid-strong base titration, the equivalence point marks the moment of complete neutralization. This point signifies the perfect balance between the opposing forces of acidity and basicity.

The Symphony of Ions: A Closer Look at Neutralization

The neutralization reaction unfolds like a carefully orchestrated symphony of ions. As H+ ions migrate from the acid to the base, the acid’s strength diminishes, while the base’s strength increases. This delicate dance continues until the equivalence point is reached, where the number of H+ ions donated by the acid equals the number of H+ ions accepted by the base.

At this point of equilibrium, the solution is neither acidic nor basic but rather neutral, with a pH of 7. The salt formed in the reaction dissolves into its constituent ions, contributing to the overall ionic strength of the solution.

Calculating pH at Equivalence Point: A Comprehensive Guide

In the realm of acid-base chemistry, understanding the pH at the equivalence point is crucial for accurate pH determination. This guide will delve into the intricacies of calculating pH at the equivalence point, empowering you with the knowledge to tackle acid-base problems with precision.

The Concept of Equivalence Point

Equivalence point marks the moment when an acid and a base react completely, resulting in the neutralization of both. At this point, the moles of acid are equal to the moles of base added. The equivalence point is often visually identified as the steepest section on the titration curve.

pH at Equivalence Point

The pH at the equivalence point varies depending on the strength of the acid and base involved. For a strong acid and a strong base (e.g., HCl and NaOH), the pH is 7.0, indicating a neutral solution. However, for a weak acid and a strong base, the pH will be greater than 7.0.

Henderson-Hasselbalch Equation

For weak acids, the Henderson-Hasselbalch (HH) equation provides a powerful tool for calculating pH:

pH = pKa + log([A-]/[HA])

where:

• pKa is the dissociation constant of the weak acid
• [A-] is the concentration of the conjugate base
• [HA] is the concentration of the weak acid

Calculating pH at Equivalence Point (Weak Acid-Strong Base Titration)

At the equivalence point in a weak acid-strong base titration, the concentration of the conjugate base is equal to the initial concentration of the weak acid. Substituting this relationship into the HH equation, we derive the formula for pH at the equivalence point:

pH = pKa + log(1)

pH = pKa

Steps for Calculating pH at Equivalence Point

1. Determine the pKa of the weak acid.
2. Substitute the pKa value into the formula: pH = pKa.
3. Calculate the pH at the equivalence point.

Example

Suppose we have a solution of acetic acid (CH3COOH) with a pKa of 4.76. To find the pH at the equivalence point in a titration with NaOH, we simply substitute the pKa into the formula:

pH = 4.76

Understanding the concepts of equivalence point and HH equation empowers you to accurately calculate pH at the equivalence point in acid-base titrations. This knowledge is invaluable for various chemical applications, including acid-base reactions, buffer preparation, and analytical chemistry.