A Comprehensive Guide To Solving Sss Triangles: A Systematic Approach
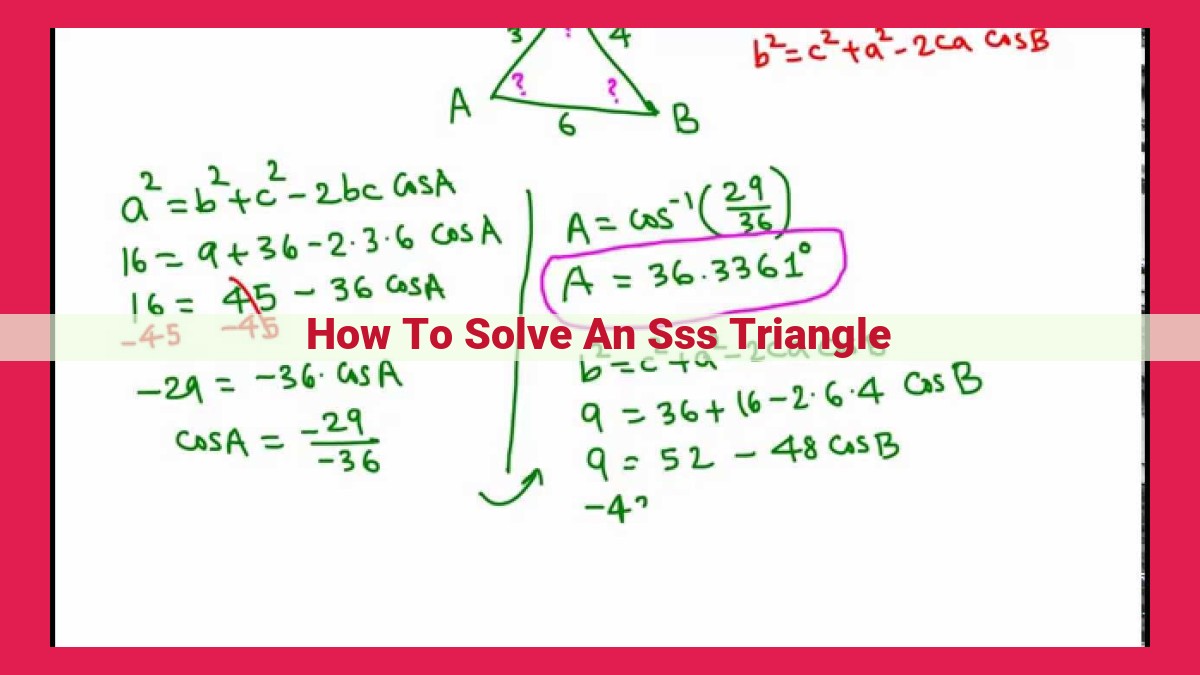
To solve an SSS triangle (one with three known side lengths), use a systematic approach:
- Apply the Law of Cosines to find one angle using two sides and their included angle.
- Use the Law of Sines to find the remaining two angles.
- Determine the half-angles using the Half-Angle Formula.
- Calculate the area using the Area Formula.
Buckle up, dear reader, as we embark on an enigmatic journey into the realm of SSS triangles. These elusive geometric shapes have baffled math enthusiasts for centuries, but fear not, for we shall unravel their secrets with a touch of storytelling magic.
An SSS triangle, as its name suggests, is a triangle where the lengths of all three sides are known. But don’t be fooled by their seemingly straightforward nature. Solving SSS triangles without advanced techniques is like navigating a labyrinth without a map—a daunting task indeed.
Their enigmatic nature stems from the fact that the traditional methods of trigonometry, such as the Law of Sines and Law of Cosines, only provide us with two pieces of information at a time: either an angle and two sides or two angles and one side. For SSS triangles, we are left with a tantalizing puzzle—determining both angles and all three side lengths.
The Law of Cosines: A Bridge to Unraveling SSS Triangles
When it comes to solving triangles, SSS triangles stand as a unique challenge. Unlike their counterparts, they lack angles to guide our calculations. However, with the advent of the Law of Cosines, this mathematical enigma unravels, allowing us to delve into the captivating world of SSS triangles.
The Law of Cosines, also known as the law of cosine rule, is a fundamental theorem that weaves together the fabric of geometry and trigonometry. Its formula, etched in the annals of mathematical lore, states the following:
**c^2 = a^2 + b^2 - 2ab*cos(C)**
where:
- c represents the length of the side opposite to angle C
- a and b are the lengths of the other two sides
- C is the angle opposite to side c
- cos(C) is the cosine of angle C
This formula unveils a profound relationship between the side lengths and the cosine of an angle in a triangle. By skillfully manipulating this equation, we can unlock a plethora of insights into SSS triangles.
The Law of Cosines holds the key to determining the lengths of unknown sides and angles within SSS triangles. Armed with this knowledge, we can embark on a journey of exploration, unraveling the mysteries that lie within these geometric wonders.
Exploring the Law of Sines: A Complementary Approach to Solving SSS Triangles
In the realm of trigonometry, the Law of Sines stands as a beacon of hope for those seeking to unravel the mysteries of SSS triangles—triangles where only the side lengths are known. Unlike its elusive counterpart, the Law of Cosines, the Law of Sines offers a more accessible path to understanding these enigmatic shapes.
The Law of Sines, in its profound simplicity, states that in any triangle, the ratio of the length of a side to the sine of the opposite angle is constant. This constant is referred to as the sine ratio.
a/sin A = b/sin B = c/sin C
Where:
- a, b, c represent the side lengths
- A, B, C represent the opposite angles to the respective sides
The Law of Sines empowers us to connect the interplay between side lengths and angles, granting us the ability to determine unknown side lengths or angles when given limited information.
Consider this example: we have an SSS triangle with sides a = 10, b = 12, c = 15. To find the measure of angle A, we use the Law of Sines:
a/sin A = c/sin C
Substituting the known values:
10/sin A = 15/sin C
Using a calculator, we solve for sin A and find that A = 30 degrees.
The Law of Sines serves as a valuable tool in the trigonometrician’s arsenal, providing a complementary approach to the Law of Cosines. By understanding the Law of Sines, we unlock a new dimension in our ability to solve SSS triangles with confidence.
Harnessing the Power of the Half-Angle Formula
In the realm of trigonometry, the Half-Angle Formula emerges as a powerful tool for unveiling the mysteries of SSS triangles. This remarkable formula allows us to determine the trigonometric functions of half an angle, paving the way for a comprehensive understanding of these elusive geometric shapes.
The Half-Angle Formula, expressed as:
sin(θ/2) = ±√[(1 - cosθ) / 2]
connects the trigonometric sine function of an angle θ to the cosine function of the same angle. By employing this formula, we can effortlessly calculate the sine of half an angle, even when the full angle’s trigonometric function is unknown.
Furthermore, the Half-Angle Formula extends its influence to other trigonometric functions. Through the following relationships:
cos(θ/2) = ±√[(1 + cosθ) / 2]
and
tan(θ/2) = ±√[((1 - cosθ) / (1 + cosθ))]
we can derive the cosine and tangent functions of half an angle, respectively.
The versatility of the Half-Angle Formula extends beyond its ability to determine individual trigonometric functions. This formula also serves as a bridge between the side lengths and angles of SSS triangles. By utilizing the following relationship derived from the Half-Angle Formula:
h = 2r / cos(θ/2)
where h represents the height of the triangle and r denotes the radius of the inscribed circle, we can establish a direct connection between the side lengths and angles of SSS triangles. This relationship empowers us to unravel the mysteries of these complex geometrical figures.
The Area Formula: Measuring the Encompassing Space
In the world of triangles, the Area Formula empowers us to determine the amount of space they encompass, providing a measure of their interior expanse. This formula unveils a crucial relationship between the side lengths of a triangle and its area.
The formula is expressed as:
Area = √(s(s-a)(s-b)(s-c))
where:
- s is the semiperimeter, which is half the sum of the three side lengths:
s = (a + b + c)/2 - a, b, and c are the lengths of the three sides
This formula highlights the interdependence of the area with the side lengths. As the side lengths increase or decrease, the area of the triangle proportionately changes. This relationship is particularly evident in equilateral triangles, where all sides are equal, resulting in maximum area.
To calculate the area using this formula, we simply plug in the known side lengths, calculate the semiperimeter, and solve for the square root. For instance, if a triangle has sides of length 5, 7, and 9, its area would be:
s = (5 + 7 + 9)/2 = 10.5
Area = √(10.5(10.5-5)(10.5-7)(10.5-9)) = 21.21 sq. units
The Area Formula serves as an invaluable tool in various fields, including engineering, architecture, and geometry. It enables us to determine the occupational space of triangular structures, the coverage area of triangular roofs, and the enclosed area of triangular parcels of land.
Solving SSS Triangles: Embark on a Trigonometric Adventure
Step 1: Uncover the Truth with the Law of Cosines
Begin by embracing the Law of Cosines, a powerful tool for deciphering triangles. This formula reveals the hidden relationship between side lengths and the cosine of an angle, allowing you to determine an unknown angle or side.
Step 2: Dance with the Law of Sines
Next, gracefully introduce the Law of Sines, a complementary formula that focuses on the side lengths and sines of the opposite angles. This formula provides additional insights into the enigmatic triangle.
Step 3: Harness the Magic of the Half-Angle Formula
Harness the power of the Half-Angle Formula, a trigonometrical gem that unveils the secrets of half angles. This formula holds the key to determining trigonometric functions for angles less than 90 degrees.
Step 4: Measure the Embracing Space: The Area Formula
Unveiling the Area Formula empowers you to calculate the area of a triangle based on its side lengths. This formula provides a comprehensive understanding of the triangle’s encompassing space.
Step 5: Triumph Over SSS Triangles: A Systematic Approach
Now, gather your knowledge and embark on the five-step journey to conquer SSS triangles:
- Determine the unknown angle using the Law of Cosines.
- Calculate the remaining angles using the Law of Sines.
- Utilize the Half-Angle Formula to find trigonometric functions for half angles.
- Calculate the area using the Area Formula.
- Celebrate your triumph over the daunting SSS triangle.
With these strategies in your arsenal, you are now equipped to navigate the realm of SSS triangles with confidence. May your trigonometric adventures be filled with enlightenment and joy!